
Læs til eksamen National gymnasieeksamen (Og enten) er et vigtigt skridt for dem, der ønsker at søge ledige stillinger på universitetskurser. Men denne fase af undersøgelser er ikke altid så let.
På matematik, vanskeligheder med at udføre beregninger hurtigt, da testen er omfattende og tiden er kort, og at huske de forskellige matematiske formler er nogle af de vigtigste klager fra studerende.
se mere
Studerende fra Rio de Janeiro vil konkurrere om medaljer ved OL...
Institut for Matematik er åben for tilmelding til OL...
Med det i tankerne udarbejdede vi denne tekst med matematiske tips og tricks til fjenden til dig, der gerne vil bestå til eksamen!
Vi har udvalgt nogle værdifulde tips til dig, der skal tage Enem. Tjek det ud nedenfor!
På Gang med 10, 100 og 1000 eller enhver anden potens af 10, er der nogle strategier, der vil fremskynde og forenkle beregningerne i Enem-testen.
Til hele tal, skal du blot tilføje nuller til højre for tallet:
56 × 10 = 560
56 × 100 = 5600
56 × 1000 = 56000
Til decimaltal, skal du blot flytte decimaltegnet til højre i henhold til antallet af nuller:
9,853 × 10 = 98,53
9,853 × 100 = 985,3
9,853 × 1000 = 9853, = 9853
På division med 10, 100 og 1000 eller enhver anden styrke på 10, er der også nogle strategier, der vil bringe dig tættere på at klare dig godt i Enem.
Når begge tal slutter på nul, kan vi annullere nullerne, hvilket gør det nemmere at tælle:
350: 10 = 35: 1 = 35
600: 100 = 6: 1 = 6
29000: 1000 = 29: 1 = 29
Til decimaltal, flyt bare decimaltegnet til venstre i henhold til antallet af nuller:
256,7: 10 = 25,67
256,7: 100 = 2,567
256,7: 1000 = ,2567 = 0,2567
For at være mere forberedt med divisionsregnskaber, læs vores tekst: Tips og tricks til divisionsberegninger.
EN bhaskaras formel er en af de mest berømte inden for matematik, men den anses også for at være en af de sværeste at huske og bruge af mange gymnasieelever.
Et alternativ til Bhaskaras formel for at finde rødderne til en 2. grads ligning, og sum og produktmetode.
Sum (S) og produkt (P):
S = -b/a og P = c/a
Beregn S og P ud fra ligningens koefficienter, og rødderne er to tal, hvis sum er S og produktet er P.
Eksempel:
x² – 3x – 10
S = -(-3)/1 = 3 og P = -10/1 = -10
Rødderne er 5 og -2, fordi 5. -2 = -10 og 5 + (-2) = 3.
Nedenfor præsenterer vi nogle tricks til at hjælpe dig med at huske meget nyttige matematiske formler og huske dem under Enem-testen.
At huske positionen af sinus, cosinus og tangens ved trigonometrisk cirkel, husk blot følgende rim:
"Sinus stående, cosinus liggende og tangent på siden."
Til trigonometriske forhold ved retvinklet trekant involverer de modsatte og tilstødende ben og hypotenusen. For ikke at blive forvirret med de tre formler skal du huske følgende sætning:
"Jeg løb og faldt på cola."
sinus = co/Hejp → løb
Cosinus = Her/Hejp → falde
Tangent = co/Her → Cola
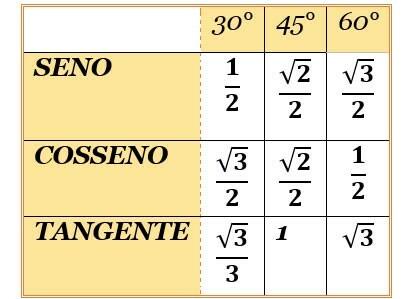
Bemærkelsesværdige vinkler er vinklerne på 30°, 45° og 60°. Det hedder de, netop fordi de er så brugte. Så du skal huske værdierne af sinus- og cosinusfunktionerne for disse vinkler.
Som? Der er en simpel sang:
"Et to tre.
Tre to en.
Nedenunder er alle to.
Rod, hvor der ikke er nogen."
Husk denne sang, bare saml bordet, og der er ingen fejl! For at finde tangentværdierne skal du bare dividere sinus med cosinus.
Starter ved bueadditions- og subtraktionsformler, kan mange geometriproblemer løses. Men i alt er der fire formler, og de er meget ens.
For ikke at blive forvirret skal du huske følgende sætning for sinus:
Sæt dig ned, krads! Sæt dig ned, krads!
Sin (a + b) = synd a. cos b + sin b. fordi en
Sin(a – b) = synd a. cos b – sin b. fordi en
Nu til cosinus:
Kløe, kløe! Sid, sid!
Cosinus (a + b) = cos a. cos b + sin a. uden b
Cosinus (a – b) = cos a. cos b – sin a. uden b
Kombinatorisk analyse falder normalt meget i Enem-testen. Derfor er det vigtigt at kende formlerne for arrangement og kombination, som gør det muligt at beregne antallet af mulige klynger, der kan dannes med i alt elementer i forskellige situationer.
For at huske disse formler kan du blot huske to sætninger. For arrangement er sætningen:
"ENstadig ntil Pknogle. Ingentil! Ingentil Pknogle!"
Og til kombination:
"Wven ntil Pode. Ingentil! Pode! Ingentil Pode!"
aritmetisk progression (PA) er den type sekvens, der falder mest i test. Formlen for det generelle udtryk for en AP kan huskes fra følgende sætning:
“ENstadig ntil Detarrangeret 1nelskede ric!"
“si nelsket? ENarrangere 1nelskede næg og dele til ndu to!”
Du kan også være interesseret:

