Μελέτη για τις εξετάσεις Πανελλήνιες εξετάσεις Λυκείου (Και είτε) είναι ένα σημαντικό βήμα για όσους επιθυμούν να υποβάλουν αίτηση για κενές θέσεις σε πανεπιστημιακά μαθήματα. Ωστόσο, αυτό το στάδιο σπουδών δεν είναι πάντα τόσο εύκολο.
Στο μαθηματικά, δυσκολίες στην γρήγορη εκτέλεση των υπολογισμών, καθώς το τεστ είναι εκτεταμένο και ο χρόνος μικρός και η απομνημόνευση των διαφόρων μαθηματικούς τύπους είναι μερικά από τα κύρια παράπονα των μαθητών.
δείτε περισσότερα
Μαθητές από το Ρίο ντε Τζανέιρο θα αγωνιστούν για μετάλλια στους Ολυμπιακούς…
Ανοιχτό για εγγραφές για τους Ολυμπιακούς Αγώνες το Μαθηματικό Ινστιτούτο…
Με αυτό κατά νου, ετοιμάσαμε αυτό το κείμενο με μαθηματικές συμβουλές και κόλπα για τον εχθρό για εσάς που θέλετε να πετύχετε στις εξετάσεις!
Επιλέξαμε μερικές πολύτιμες συμβουλές για εσάς που πρόκειται να πάρετε το Enem. Δείτε το παρακάτω!
Στο Πολλαπλασιάστε με το 10, το 100 και το 1000 ή οποιαδήποτε άλλη δύναμη του 10, υπάρχουν ορισμένες στρατηγικές που θα επιταχύνουν και θα απλοποιήσουν τους υπολογισμούς στο τεστ Enem.
Για ολόκληροι αριθμοί, απλά προσθέστε μηδενικά στα δεξιά του αριθμού:
56 × 10 = 560
56 × 100 = 5600
56 × 1000 = 56000
Για δεκαδικοί αριθμοί, απλώς μετατοπίστε την υποδιαστολή προς τα δεξιά σύμφωνα με τον αριθμό των μηδενικών:
9,853 × 10 = 98,53
9,853 × 100 = 985,3
9,853 × 1000 = 9853, = 9853
Στο διαίρεση με το 10, το 100 και το 1000 ή οποιαδήποτε άλλη δύναμη του 10, υπάρχουν επίσης ορισμένες στρατηγικές που θα σας φέρουν πιο κοντά στο να τα πάτε καλά στο Enem.
Όταν και οι δύο αριθμοί τελειώνουν σε μηδέν, μπορούμε να ακυρώσουμε τα μηδενικά, διευκολύνοντας την μέτρηση:
350: 10 = 35: 1 = 35
600: 100 = 6: 1 = 6
29000: 1000 = 29: 1 = 29
Για δεκαδικοί αριθμοί, απλώς μετακινήστε την υποδιαστολή προς τα αριστερά σύμφωνα με τον αριθμό των μηδενικών:
256,7: 10 = 25,67
256,7: 100 = 2,567
256,7: 1000 = ,2567 = 0,2567
Για να είστε πιο προετοιμασμένοι με τους λογαριασμούς τμημάτων, διαβάστε το κείμενό μας: Συμβουλές και κόλπα για υπολογισμούς διαίρεσης.
ΕΝΑ ο τύπος του bhaskara είναι ένα από τα πιο γνωστά στα μαθηματικά, αλλά θεωρείται επίσης ένα από τα πιο δύσκολα στην απομνημόνευση και χρήση από πολλούς μαθητές γυμνασίου.
Μια εναλλακτική στον τύπο του Bhaskara για την εύρεση των ριζών του α εξίσωση 2ου βαθμού, και το άθροισμα και μέθοδος προϊόντος.
Άθροισμα (S) και γινόμενο (Ρ):
S = -b/a και P = c/a
Υπολογίστε τα S και P από τους συντελεστές της εξίσωσης και οι ρίζες είναι δύο αριθμοί των οποίων το άθροισμα είναι S και το γινόμενο είναι P.
Παράδειγμα:
x² – 3x – 10
S = -(-3)/1 = 3 και P = -10/1 = -10
Οι ρίζες είναι 5 και -2, γιατί 5. -2 = -10 και 5 + (-2) = 3.
Παρακάτω, παρουσιάζουμε μερικά κόλπα που θα σας βοηθήσουν να απομνημονεύσετε πολύ χρήσιμους μαθηματικούς τύπους και να τους θυμάστε κατά τη διάρκεια του τεστ Enem.
Για να θυμηθούμε τη θέση του ημίτονο, συνημίτονο και εφαπτομένη στο τριγωνομετρικός κύκλος, απλώς απομνημονεύστε την παρακάτω ομοιοκαταληξία:
«Ημιτόνου όρθιο, συνημίτονο ξαπλωμένο και εφαπτομένη στο πλάι».
Στο τριγωνομετρικές αναλογίες στο ορθογώνιο τρίγωνο εμπλέκουν τα απέναντι και παρακείμενα πόδια και την υποτείνουσα. Για να μην μπερδευτείτε με τους τρεις τύπους, απομνημονεύστε την ακόλουθη πρόταση:
«Έτρεξα και έπεσα πάνω στην κόκα».
ημίτονο = συν/γειαp → έτρεξε
Συνημίτονο = Εδώ/γειαp → πτώση
Εφαπτομένη = συν/Εδώ → Οπτάνθρακα
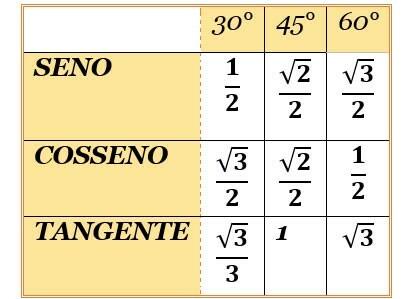
Αξιοσημείωτες γωνίες είναι οι γωνίες 30°, 45° και 60°. Ονομάζονται έτσι, ακριβώς επειδή χρησιμοποιούνται τόσο. Επομένως, πρέπει να απομνημονεύσετε τις τιμές των συναρτήσεων ημιτονοειδούς και συνημιτονοειδούς αυτών των γωνιών.
Οπως και? Υπάρχει ένα απλό τραγούδι:
"Ενα δύο τρία.
Τρία δύο ένα.
Από κάτω είναι και τα δύο.
Ρίζα όπου δεν υπάρχει».
Θυμηθείτε αυτό το τραγούδι, απλά συναρμολογήστε το τραπέζι και δεν υπάρχει λάθος! Για να βρείτε τις εφαπτομενικές τιμές, απλώς διαιρέστε το ημίτονο με το συνημίτονο.
Ξεκινώντας στις τύποι πρόσθεσης και αφαίρεσης τόξου, πολλά προβλήματα γεωμετρίας μπορούν να λυθούν. Ωστόσο, συνολικά, υπάρχουν τέσσερις τύποι και μοιάζουν πολύ.
Για να μην μπερδεύεστε, απομνημονεύστε την ακόλουθη πρόταση για το ημιτονικό:
Κάτσε, ξύσε! Κάτσε, ξύσε!
Αμαρτία (α + β) = αμαρτία α. cos b + αμαρτία β. cos α
Sin(a – b) = αμαρτία α. cos b – αμαρτία β. cos α
Τώρα για το συνημίτονο:
Φαγούρα, φαγούρα! Κάτσε, κάτσε!
Συνημίτονο (α + β) = συν α. cos b + αμαρτία α. χωρίς β
Συνημίτονο (α – β) = συν α. cos b – αμαρτία α. χωρίς β
Συνδυαστική ανάλυση συνήθως πέφτει πολύ στο τεστ Enem. Επομένως, είναι απαραίτητο να γνωρίζετε τους τύπους του διάταξη και συνδυασμός, που επιτρέπουν τον υπολογισμό του αριθμού των πιθανών συστάδων που μπορούν να σχηματιστούν με ένα σύνολο στοιχείων σε διαφορετικές καταστάσεις.
Για να απομνημονεύσετε αυτούς τους τύπους, μπορείτε απλώς να απομνημονεύσετε δύο προτάσεις. Για τη διευθέτηση, η πρόταση είναι:
"ΕΝΑακόμη nστο Ποστό. Οχιστο! Οχιστο Ποστό!"
Και για συνδυασμό:
"Wφίλος nστο Πωδή. Οχιστο! Πωδή! Οχιστο Πωδή!"
αριθμητική πρόοδος (PA) είναι ο τύπος ακολουθίας που πέφτει περισσότερο στις δοκιμές. Ο τύπος για τον γενικό όρο ενός AP μπορεί να θυμηθεί από την ακόλουθη πρόταση:
“ΕΝΑακόμη nστο οδιατεταγμένα 1nαγαπητός ric!”
“μικρόσε nαγαπήθηκε; ΕΝΑκανονίζω 1nαγαπητός nαυγό και διαιρέστε Για nεσείς δύο!”
Μπορεί επίσης να σας ενδιαφέρει: