Ο υπόλοιπο είναι ένα από τα τέσσερα στοιχεία που απαρτίζουν το αλγόριθμος διαίρεσης. Είναι η τιμή που απομένει για το πηλίκο να είναι ένα. ακέραιος αριθμός.
Όταν το υπόλοιπο είναι ίσο με μηδέν, λέμε ότι η διαίρεση είναι ακριβής. Στην περίπτωση αυτή, το μέρισμα ισούται με το γινόμενο του διαιρέτη και του πηλίκου:
δείτε περισσότερα
Μαθητές από το Ρίο ντε Τζανέιρο θα αγωνιστούν για μετάλλια στους Ολυμπιακούς…
Ανοιχτό για εγγραφές για τους Ολυμπιακούς Αγώνες το Μαθηματικό Ινστιτούτο…
μέρισμα = διαιρέτης × πηλίκο
Ωστόσο, υπάρχουν περιπτώσεις όπου το υπόλοιπο είναι μια μη μηδενική τιμή. Δείτε ένα παράδειγμα:
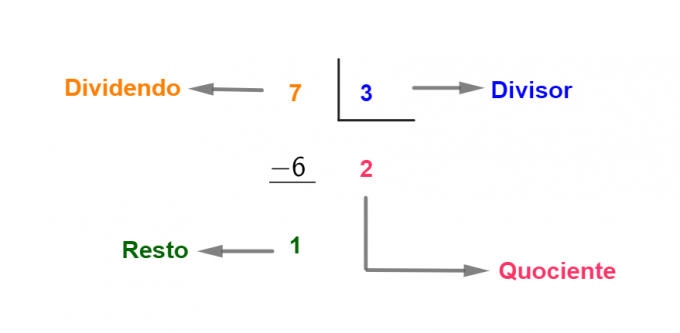
Στην περίπτωση αυτή, το μέρισμα είναι ίσο με το γινόμενο του διαιρέτη και του πηλίκου συν το υπόλοιπο:
μέρισμα = (διαιρέτης × πηλίκο) + υπόλοιπο
Αλλά τελικά, σε τι χρησιμεύει το υπόλοιπο τμήμα? Τι σημαίνει αυτή η τιμή που απομένει; Θα τα εξηγήσουμε όλα παρακάτω!
Θα εξηγήσουμε σε τι χρησιμεύει το υπόλοιπο της διαίρεσης μέσω ενός μαθηματικού προβλήματος που θα περιλαμβάνει δύο καταστάσειςπολλά διαφορετικά.
Θα δείτε ότι, αν και ο λογαριασμός διαίρεσης είναι ο ίδιος στην επίλυση των δύο καταστάσεων, το υπόλοιπο θα έχει διαφορετικό νόημα σε κάθε μία.
Πρόβλημα:
Ένας ζαχαροπλάστης παράγει brigadeiros και τα πουλάει σε κουτιά που χωρούν το πολύ 50 γλυκά.

Ας υποθέσουμε ότι μια συγκεκριμένη ημέρα παρήγαγε 384 μονάδες.
Κατάσταση 1: Μια πελάτισσα αγοράζει όλα τα κλειστά κουτιά που έχει εκείνη την ημέρα. Τα κλειστά κουτιά είναι τα κουτιά που περιέχουν τον μέγιστο αριθμό καραμελών.
Πόσα κουτιά θα λάβει αυτός ο πελάτης;
Ανάλυση:
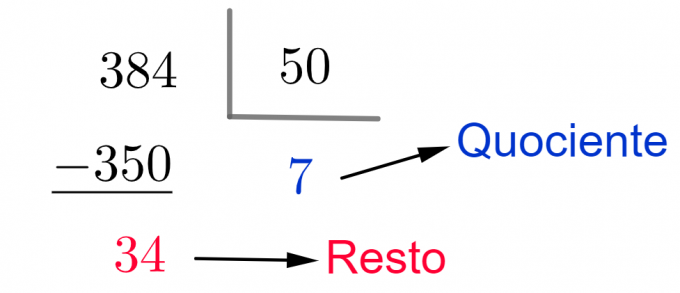
Το πηλίκο σε αυτόν τον λογαριασμό αντιπροσωπεύει τον αριθμό των κλειστών πλαισίων. Το υπόλοιπο δείχνει την ποσότητα των καραμελών που απομένουν πριν συμπληρώσετε ένα νέο κουτί.
Καθώς ο πελάτης θέλει να αγοράσει μόνο κλειστά κουτιά, τότε θα λάβει 7 κουτιά.
Σημειώστε ότι τα υπόλοιπα δεν επηρεάζουν τον αριθμό των κουτιών, καθώς τα κουφέτα που έχουν απομείνει δεν θα πωληθούν σε αυτόν τον πελάτη.
Κατάσταση 2: Μια πελάτισσα αγοράζει όλα τα γλυκά που έχει εκείνη την ημέρα.
Πόσα κουτιά θα λάβει αυτός ο πελάτης;
Ανάλυση:

Σε αυτή την περίπτωση, ο πελάτης θα αγοράσει όλα τα γλυκά, οπότε και όσα έχουν απομείνει θα τοποθετηθούν σε κουτί.
Με αυτόν τον τρόπο, ο πελάτης θα λάβει 8 κουτιά, εκ των οποίων τα 7 είναι κλειστά και ένα άλλο κουτί με 34 καραμέλες.
Σε αντίθεση με την κατάσταση 1, εδώ το υπόλοιπο παρεμβαίνει στον αριθμό των πλαισίων.
Τι συμπέρασμα μπορούμε να συμπεράνουμε από αυτό το πρόβλημα;
Το υπόλοιπο σε μια διαίρεση θα έχει διαφορετική σημασία ανάλογα με κάθε τύπο προβλήματος. Σε ορισμένες περιπτώσεις μπορεί να αγνοηθεί, σε άλλες όχι.
Μπορεί επίσης να σας ενδιαφέρει:

