Exercises on proportional segments

click fraud protection

When the ratio of two line segments is equal to the ratio of two other segments, they are called proportional segments.

A reason between two segments is obtained by dividing the length of one by the other.

Students from Rio de Janeiro will compete for medals at the Olympics…

The Institute of Mathematics is open for registration for the Olympics…

Thus, given four proportional line segments with lengths The, B, w It is d, in that order, we have a proportion:

$\dpi{120} \mathbf{\frac{a}{b} \frac{c}{d}}$

And, by the fundamental property of proportions, we have $\dpi{120} \mathbf{ ad cb}$ .

To learn more, check out a list of exercises on proportional segments, with all questions resolved!

Exercises on proportional segments

Question 1. The segments $\dpi{120} \overline{AB}, \overline{CD}, \overline{EF}\, \mathrm{e}\, \overline{GH}$ are, in that order, proportional segments. Determine the measure of $\dpi{120} \overline{CD}$ knowing that $\dpi{120} \overline{AB} 5$ , $\dpi{120} \overline{EF} 7.5$ It is $\dpi{120} \overline{GH} 13.8$ .

Question 2. Determine $\dpi{120} \overline{BC}$ knowing that $\dpi{120} \frac{\overline{AB}}{7} \frac{\overline{BC}}{4}$ is that:

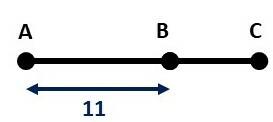
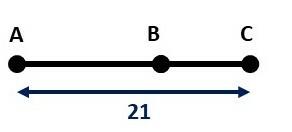
Question 3. Determine $\dpi{120} \overline{AB}$ knowing that $\dpi{120} \frac{\overline{AB}}{2} \frac{\overline{BC}}{5}$ is that:

Question 4. Determine the lengths of the sides of a triangle that has a perimeter of 52 units and whose sides are proportional to the sides of another triangle with lengths 2, 6, and 5.

instagram story viewer

Resolution of question 1

If the segments $\dpi{120} \overline{AB}, \overline{CD}, \overline{EF}\, \mathrm{e}\, \overline{GH}$ are, in that order, proportional segments, then:

$\dpi{120} \frac{\overline{AB}}{\overline{CD}} \frac{\overline{EF}}{\overline{GH}}$

replacing $\dpi{120} \overline{AB} 5$ , $\dpi{120} \overline{EF} 7.5$ It is $\dpi{120} \overline{GH} 13.8$ , We have to:

$\dpi{120} \frac{5}{\overline{CD}} \frac{7,5}{13,8}$

Applying the fundamental property of proportions:

$\dpi{120} \Rightarrow 7.5 \cdot \overline{CD} 69$

$\dpi{120} \Rightarrow \overline{CD} \frac{69}{7.5}$

$\dpi{120} \Rightarrow \overline{CD} 9.2$

Resolution of question 2

We have:

$\dpi{120} \frac{\overline{AB}}{7} \frac{\overline{BC}}{4}$

replacing $\dpi{120} \overline{AB} 11$ , We have to:

$\dpi{120} \frac{11}{7} \frac{\overline{BC}}{4}$

Applying the fundamental property of proportions:

$\dpi{120} \Rightarrow 7\overline{BC} 44$

$\dpi{120} \Rightarrow \overline{BC} \frac{44}{7}$

$\dpi{120} \Rightarrow \overline{BC} \approx 6.28$

Resolution of question 3

We have:

$\dpi{120} \frac{\overline{AB}}{2} \frac{\overline{BC}}{5}$

As $\dpi{120} \overline{AB} + \overline{BC} 21$ , then, $\dpi{120} \overline{AB} 21 - \overline{BC}$ . Substituting in the above expression, we have:

$\dpi{120} \frac{21-\overline{BC}}{2} \frac{\overline{BC}}{5}$

Applying the fundamental property of proportions:

$\dpi{120} \Rightarrow 2\overline{BC} 5(21- \overline{BC})$

$\dpi{120} \Rightarrow 2\overline{BC} 105- 5\overline{BC}$

$\dpi{120} \Rightarrow 7\overline{BC} 105$

$\dpi{120} \Rightarrow \overline{BC} \frac{105}{7}$

$\dpi{120} \Rightarrow \overline{BC} 15$

Soon $\dpi{120} \overline{AB} 21 - \overline{BC} 21 - 15 6$ .

Resolution of question 4

Making a representative drawing, we can see that $\dpi{120} \overline{AB} + \overline{BC} + \overline{AC} 52$ .

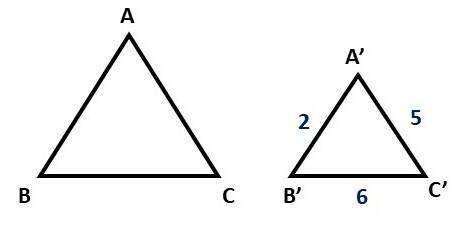
Since the sides of the triangles are proportional, we have:

$\dpi{120} \frac{\overline{AB}}{2} \frac{\overline{BC}}{6} \frac{\overline{AC}}{5} r$

Being $\dpi{120} r$ the ratio of proportionality.

Furthermore, if the sides are proportional, their sum, that is, the perimeters, are also:

$\dpi{120} \frac{\overline{AB} + \overline{BC} +\overline{AC} }{2 + 6 + 5} r$

$\dpi{120} \Rightarrow \frac{52 }{13} r$

$\dpi{120} \Rightarrow r 4$

From the ratio of proportionality and the known sides, we obtain the measures of the sides of the other triangle:

$\dpi{120} \overline{AB} r\cdot \overline{A'B'} 4\cdot 2 8$

$\dpi{120} \overline{BC} r\cdot \overline{B'C'} 4\cdot 6 24$

$\dpi{120} \overline{AC} r\cdot \overline{A'C'} 4\cdot 5 20$

To download this list of exercises on proportional segments in PDF, click here!

You may also be interested:

similarity of triangles
Thales Theorem
List of exercises on similarity of triangles
List of exercises on ratio and proportion
List of exercises on Thales' theorem

Global actress offers math classes to Enem candidates

on Aug 03, 2023

Exercises on proportional segments

Exercises on proportional segments

Resolution of question 1

Resolution of question 2

Resolution of question 3

Resolution of question 4

Exercises on interspecific ecological relationships

Verbs with the letter Q

Global actress offers math classes to Enem candidates