O barycenter of a triangle is the meeting point between its three medians. In the figure below, the barycenter is the G point.

see more
Students from Rio de Janeiro will compete for medals at the Olympics…
The Institute of Mathematics is open for registration for the Olympics…
You trianglesare three-sided polygons, which can be classified according to the measures of the sides or according to the measures of the interior angles.
However, regardless of the type, any triangle always has three medians.
Each of the triangle's medians is a line segment that connects a vertex to the midpoint of the opposite side.
The midpoint of a segment is the point that is exactly in the middle of the segment.
To find the coordinates of the barycenter of the triangle, use the coordinates of the vertices of the triangle in the cartesian plane.
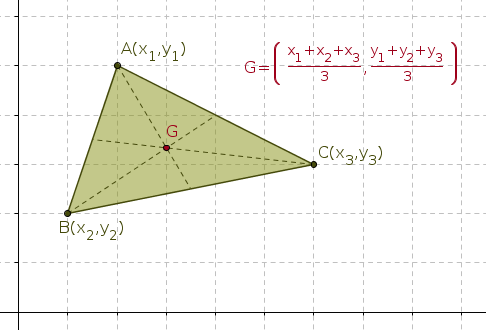
The abscissa of the barycenter is given by the mean of the abscissas of the vertices and the ordinate of the barycenter is given by the mean of the ordinates of the vertices.
In this way, being ,
,
, the vertices of the triangle and the barycenter
, we have:
It is
Example: Determine the barycenter coordinates of a triangle with vertices A(-2, 5), B(3, 3) and C(-1, -2).
Substituting the coordinates of the vertices in the presented formulas, we have:
Therefore, the barycenter is the point G(0, 2).

You may also be interested: