Practical Briot-Ruffini device

O practical Briot-Ruffini device is a method for performing the division of a polynomial by a binomial of the 1st degree.

Consider a polynomial of degree n:

Students from Rio de Janeiro will compete for medals at the Olympics…

The Institute of Mathematics is open for registration for the Olympics…

$\dpi{120} \mathbf{P(x) a_nx^n+a_{n-1}x^{n-1} + a_{n-2}x^{n-2}+...+a_2x^ 2 + a_1x+a_0}$

And a binomial of the form:

$\dpi{120} \mathbf{Q(x) x+a}$ or

$\dpi{120} \mathbf{Q(x) x-a}$

To use the Briot-Ruffini device and calculate the division of $\dpi{120} \mathbf{P(x)}$ per $\dpi{120} \mathbf{Q(x)}$ , we need the coefficients $\dpi{120} \mathbf{a_n, a_{n-1}, a_{n-2},..., a_2, a_1\,} e\, \mathbf{a_0}$ in $\dpi{120} \mathbf{P(x)}$ and from the root of $\dpi{120} \mathbf{Q(x)}$ , which is determined by solving the equation $\dpi{120} \mathbf{Q(x) 0}$ .

How does the Briot-Ruffini device work?

We will show how to calculate the division of a polynomial by a binomial using the Biot-Ruffini device, using an example.

Example:

Let's divide the polynomial $\dpi{120} \mathbf{3x^3 - 6x + 2 }$ per $\dpi{120} \mathbf{x - 2}$ .

1st step) We obtain the root of $\dpi{120} \mathbf{x - 2}$ :

$\dpi{120} \mathbf{x - 2 0}$

$\dpi{120} \Rightarrow \mathbf{x 2}$

2nd step) We check which are the coefficients of $\dpi{120} \mathbf{3x^3 - 6x + 2 }$ :

Since we have a polynomial of degree 3, we must have the coefficients $\dpi{120} \mathbf{a_3, a_2, a_1\,} e\mathbf{\, a_o}$ . as the term $\dpi{120} \mathbf{a_2x^2}$ does not appear in the polynomial, the coefficient $\dpi{120} \mathbf{a_2}$ is equal to 0.

$\dpi{120} \mathbf{{\color{Red} 3}x^3 + {\color{Blue} 0}x^2 { {\color{DarkGreen} - 6}}x + {{\color{DarkOrange } two}} }$

The coefficients are 3, 0, -6, and 2.

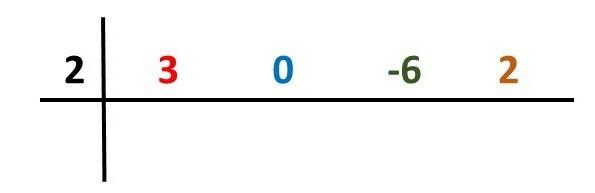
3rd step) We set up a table with the root found (2) and the coefficients (3, 0, -6 and 2):

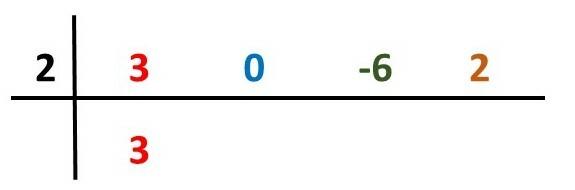
4th step) We copy the first coefficient in the bottom line:

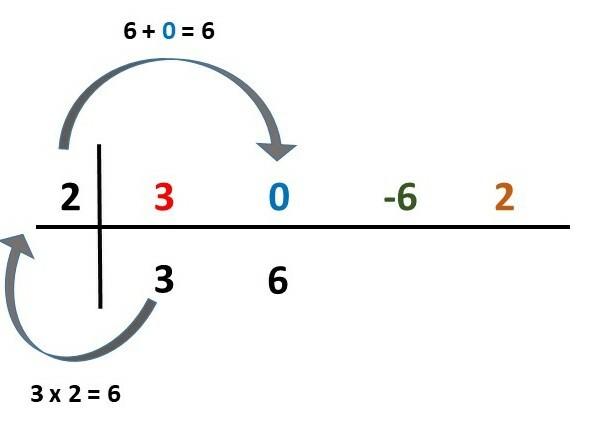
5th step) We multiply this first value (3) by the root (2) and add it to the next coefficient (0). We write the result on the bottom line.

6th step) We repeat step 5, for the second value of the bottom line.

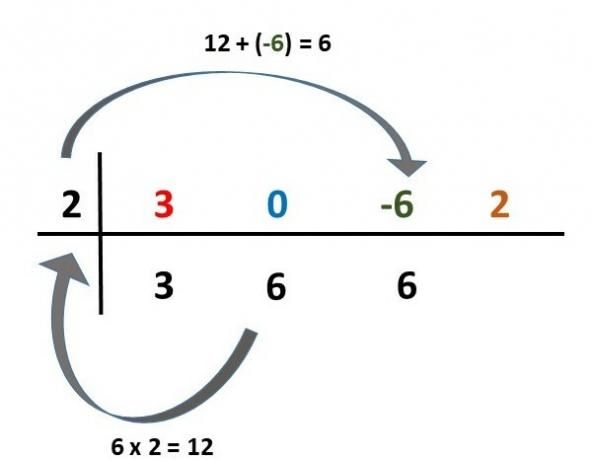
7th step) We repeat step 5, for the third value of the bottom line.

8th step) With the table already complete, the last number is the remainder of the division and the others are the coefficients of the resulting polynomial.

Rest: 14
Coefficients: 3, 6 It is 6.

9th step) We write the resulting polynomial, considering one degree less than the degree of the polynomial that we divided.

We divide a polynomial of degree 3, so the polynomial obtained will be of degree 2.

$\dpi{120} \mathbf{3x^2 + 6x + 6}$

This means that $\dpi{120} \mathbf{3x^3 - 6x + 2 (3x^2+6x+6)\cdot (x-2)+14}$ .

You may also be interested:

Division of polynomials - Key method
Multiplication of polynomials
Adding and Subtracting Polynomials
Factorization of polynomials
polynomial function

Practical Briot-Ruffini device

How does the Briot-Ruffini device work?

How much does a Physiotherapist earn?

Be careful when moving: these are the 4 WORST signs to have as a neighbor

Learn how to become a Free Market courier!