Estudia para el examen Examen Nacional de Escuela Secundaria (Y también) es un paso importante para quienes deseen postularse a vacantes en carreras universitarias. Sin embargo, esta etapa de estudios no siempre es tan fácil.
En matemáticas, dificultades para realizar cálculos rápidamente, ya que la prueba es extensa y el tiempo es corto, y memorizar los diversos fórmulas matemáticas son algunas de las principales quejas de los estudiantes.
vea mas
Estudiantes de Río de Janeiro competirán por medallas en los Juegos Olímpicos…
El Instituto de Matemáticas está abierto para inscripciones para los Juegos Olímpicos…
Con eso en mente, preparamos este texto con trucos y consejos matemáticos para el enem para ti que quieres tener éxito en el examen!
Hemos seleccionado algunos consejos valiosos para ti que vas a tomar el Enem. ¡Compruébalo a continuación!
En Multiplica por 10, 100 y 1000 o cualquier otra potencia de 10, hay algunas estrategias que acelerarán y simplificarán los cálculos en la prueba Enem.
Para números enteros, simplemente agregue ceros a la derecha del número:
56 × 10 = 560
56 × 100 = 5600
56 × 1000 = 56000
Para numeros decimales, simplemente desplaza el punto decimal a la derecha según el número de ceros:
9,853 × 10 = 98,53
9,853 × 100 = 985,3
9,853 × 1000 = 9853, = 9853
En división por 10, 100 y 1000 o cualquier otra potencia de 10, también hay algunas estrategias que te acercarán a hacerlo bien en el Enem.
Cuando ambos números terminan en cero, podemos cancelar los ceros, facilitando el conteo:
350: 10 = 35: 1 = 35
600: 100 = 6: 1 = 6
29000: 1000 = 29: 1 = 29
Para numeros decimales, simplemente mueva el punto decimal a la izquierda según el número de ceros:
256,7: 10 = 25,67
256,7: 100 = 2,567
256,7: 1000 = ,2567 = 0,2567
Para estar más preparado con las cuentas de división, lea nuestro texto: Consejos y trucos para los cálculos de división.
A fórmula de bhaskara es uno de los más famosos en matemáticas, pero también es considerado uno de los más difíciles de memorizar y utilizar por muchos estudiantes de secundaria.
Una alternativa a la fórmula de Bhaskara para encontrar las raíces de un ecuación de segundo grado, y el método de suma y producto.
Suma (S) y producto (P):
S = -b/a y P = c/a
Calcula S y P a partir de los coeficientes de la ecuación y las raíces son dos números cuya suma es S y el producto es P.
Ejemplo:
x²-3x-10
S = -(-3)/1 = 3 y P = -10/1 = -10
Las raíces son 5 y -2, porque 5. -2 = -10 y 5 + (-2) = 3.
A continuación, presentamos algunos trucos para ayudarte a memorizar fórmulas matemáticas muy útiles y recordarlas durante la prueba de Enem.
Para recordar la posición de seno, coseno y tangente en el círculo trigonométrico, solo memoriza la siguiente rima:
“Seno de pie, coseno acostado y tangente en el lado”.
Hacia razones trigonométricas en el triángulo rectángulo involucrar los catetos opuestos y adyacentes y la hipotenusa. Para no confundirse con las tres fórmulas, memoriza la siguiente oración:
“Corrí y me caí en la coca”.
seno = co/Holap → corrió
coseno = Aquí/Holapag → caer
tangente = co/Aquí → Coca-Cola
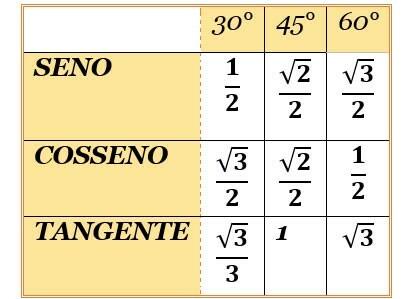
Los ángulos notables son los ángulos de 30°, 45° y 60°. Se llaman así, precisamente porque así se usan. Entonces, necesitas memorizar los valores de las funciones seno y coseno de estos ángulos.
¿Como? Hay una canción sencilla:
"Uno dos tres.
Tres dos uno.
Debajo están los dos.
Raíz donde no la hay.”
Recordando esta canción, ¡solo arma la mesa y no hay error! Para encontrar los valores de la tangente, simplemente divide el seno por el coseno.
A partir de las fórmulas de suma y resta de arco, se pueden resolver muchos problemas de geometría. Sin embargo, en total, hay cuatro fórmulas y son muy similares.
Para no confundirte, memoriza la siguiente oración para el seno:
¡Siéntate, rasca! ¡Siéntate, rasca!
Sin (a + b) = sin a. cos b + sen b. porque un
Sin(a – b) = sin a. cos b – sen b. porque un
Ahora para el coseno:
¡Pica, pica! ¡Siéntate, siéntate!
Coseno (a + b) = cos a. cos b + sen a. sin b
Coseno (a – b) = cos a. cos b – sen a. sin b
Análisis combinatorio Suele caer mucho en la prueba de Enem. Por lo tanto, es fundamental conocer las fórmulas de arreglo y combinacion, que permiten calcular el número de posibles agrupaciones que se pueden formar con un total de elementos en diferentes situaciones.
Para memorizar estas fórmulas, simplemente puede memorizar dos oraciones. Para el arreglo, la oración es:
"Aaún nortehacia PAGhueso. No¡hacia! Nohacia PAG¡hueso!"
Y para combinación:
"Wamigo nortehacia PAGoda. No¡hacia! PAG¡oda! Nohacia PAG¡oda!"
progresión aritmética (PA) es el tipo de secuencia que cae más en las pruebas. La fórmula para el término general de un AP puede recordarse de la siguiente oración:
“Aaún nortehacia Elorganizado 1norteamado ric!”
“sen norte¿amado? Aarreglar 1norteamado nortehuevo y dividir para nortetú dos!”
También te puede interesar:
