
Kun teemme tilit kertolaskunumeroissa, joissa on enemmän kuin kaksi numeroa, on tavallista jättää yksi tai useampi tyhjä väli.
Mutta tiedätkö miksi jätämme nämä tilat tyhjiksi? Ovatko ne välttämättömiä? Voitko tehdä kertolasku ilman tyhjiä välilyöntejä?
Katso lisää
Rio de Janeiron opiskelijat kilpailevat mitaleista olympialaisissa…
Matematiikan instituutti on avoinna ilmoittautumista varten olympialaisiin…
Lue eteenpäin saadaksesi vastaukset kaikkiin näihin kysymyksiin!
Selitetäänpä esimerkillä.
Laske 11 x 12
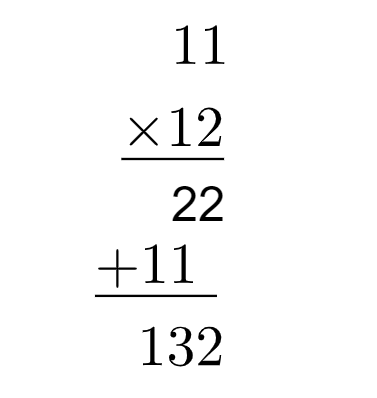
Kerromme 11:llä 2:lla ja kerromme sitten 11:llä 1:llä.
11 x 2 = 22 → kirjoitamme sen väliviivan alle.
11 x 1 = 11 → kirjoitamme edellisen tuloksen alle jättäen oikealle välilyönnin.
Lopuksi lisäämme, jolloin saadaan arvo 132.
Mutta miksi jätämme tämän tilan? Jätämme tilaa oikean vastauksen saamiseen, käytännöllisesti!
Huomaa, että 12 = 10 + 2 → yksi kymmenen plus kaksi ykköstä.
Joten 11:n kertominen 12:lla on sama kuin kertomalla 11 erikseen 10:llä ja 11:llä kahdella ja laskemalla tulokset yhteen.
11 x 10 = 110
11 x 2 = 22
Näiden tulosten lisääminen: 110 + 22 = 132. Siksi, 11 x 22 = 132.
Käytännön menetelmässä tämä tulos saadaan vain tilalla. Muuten saisimme 33, ja se olisi väärin, koska näimme jo, että 132 on oikein.
Jos tyhjät välilyönnit hämmentävät sinua suoritettaessa kertolaskujen summaa, tiedä, että tämä voidaan välttää lisäämällä jokaiseen välilyöntiin nolla.
Tämä toimii, koska todellisuudessa jokainen välilyönti vastaa itse asiassa nollaa, näimme tämän jo, kun teimme luvun 12 hajotuksen ennen kertolaskua.
Joten tilisi, johon on lisätty nolla, on oikea:

Saatat myös olla kiinnostunut:

