
इसका क्या मतलब है भिन्न को सरल बनाएं? भिन्न को सरल बनाने का अर्थ है एक समतुल्य भिन्न लिखना जिसका अंश और हर मूल भिन्न से छोटा हो।
समतुल्य भाग वे भिन्नों से अधिक कुछ नहीं हैं जो संपूर्ण की समान मात्रा या भाग का प्रतिनिधित्व करते हैं।
और देखें
रियो डी जनेरियो के छात्र ओलंपिक में पदक के लिए प्रतिस्पर्धा करेंगे...
गणित संस्थान ओलंपिक के लिए पंजीकरण के लिए खुला है...
यह कैसे काम करता है यह समझने के लिए निम्नलिखित उदाहरण पर विचार करें:
8 टुकड़ों वाले पिज़्ज़ा में, पिज़्ज़ा के आधे भाग को दर्शाने वाला अंश है . हालाँकि, यदि उसी पिज़्ज़ा को केवल 4 टुकड़ों में विभाजित किया जाता है, तो इसका आधा भाग अंश द्वारा दर्शाया जाता है
. नीचे दिया गया चित्र देखें:

अंश और हर अलग-अलग होने के बावजूद, भिन्न यह है
पिज़्ज़ा की समान मात्रा का प्रतिनिधित्व करें। इसलिए, ये भिन्न समतुल्य हैं, जिसका अर्थ है कि:
प्रश्न 1: क्या भिन्न के बराबर कोई भिन्न होता है , और भी छोटे शब्दों के साथ?
हाँ, अंश अंश के बराबर है
, क्योंकि यह पिज़्ज़ा के आधे हिस्से का भी प्रतिनिधित्व करता है, जब इसे केवल दो टुकड़ों में विभाजित किया जाता है।
अतः ये तीन भिन्न समतुल्य हैं:
नहीं, ये सबसे छोटे संभावित मान हैं, यानी हम अब इस भिन्न को सरल नहीं बना सकते।
इस मामले में, हम कहते हैं कि भिन्न और यह अघुलनशील रूप अंश का
.
पाई डिज़ाइन ने पाई के आधे हिस्से को दर्शाने के लिए छोटे शब्दों के साथ समतुल्य भिन्नों को ढूंढना आसान बना दिया।
अब, आइए एक उदाहरणात्मक छवि की सहायता के बिना भिन्नों को सरल बनाने का एक व्यावहारिक और आसान तरीका देखें।
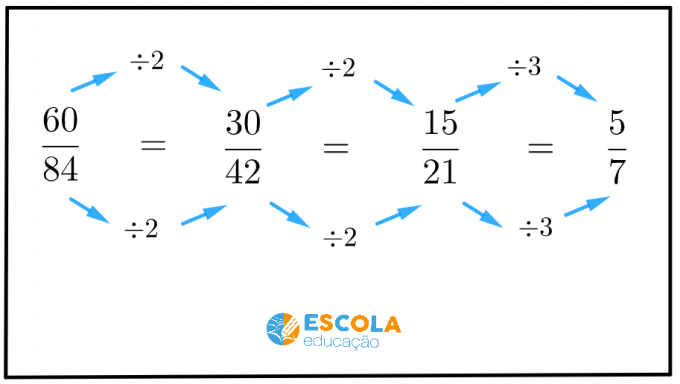
किसी भिन्न को सरल बनाने के लिए, भिन्न के अंश और हर को a से विभाजित करें एक जैसी संख्या 1 से अधिक.
1 से बड़ी पहली संख्या संख्या 2 है। क्या इस भिन्न के दोनों पद 2 से विभाज्य हैं?
दोनों संख्याएँ विभाज्य होनी चाहिए! यदि दोनों नहीं हैं, तो चलिए अगले नंबर पर चलते हैं।
अगला नंबर 3 है. क्या इस भिन्न के दोनों पद 3 से विभाज्य हैं?
तो, भिन्न को सरल बनाने के लिए, आइए अंश और हर को 3 से विभाजित करें।

इसलिए, हमें करना होगा .
सवाल: भिन्न को सरल बनाना संभव है ? नहीं, ये इस भिन्न के सबसे छोटे संभावित पद हैं।
तब, भिन्न का अपरिवर्तनीय रूप है
.

यह भी पढ़ें: