A törtek egyszerűsítése - Egyenértékű és redukálhatatlan törtek

Mit jelent tört egyszerűsítése? A tört egyszerűsítése azt jelenti, hogy egy ekvivalens törtet írunk, amelynek kisebb a számlálója és a nevezője, mint az eredeti törtnek.

Egyenértékű törtek nem mások, mint törtrészek, amelyek ugyanazt a mennyiséget vagy egy egész egy részét képviselik.

többet látni

Rio de Janeiró-i diákok érmekért küzdenek az olimpián…

A Matematikai Intézetben lehet jelentkezni az olimpiára…

Ennek megértéséhez nézze meg a következő példát:

Egy 8 darabos pizzában a pizza felét képviselő töredék az $\dpi{120} \frac{4}{8}$ . Ha azonban ugyanazt a pizzát csak 4 darabra osztjuk, akkor a felét a tört jelenti $\dpi{120} \frac{2}{4}$ . Lásd az alábbi ábrát: Egyenértékű törtek

Annak ellenére, hogy a számláló és a nevező eltérő, a törtek $\dpi{120} \frac{4}{8}$ Ez $\dpi{120} \frac{2}{4}$ ugyanannyi pizzát jelentenek. Ezért ezek a törtek egyenértékűek, ami azt jelenti, hogy:

$\dpi{120} \frac{4}{8} \frac{2}{4}$

1. kérdés: Van-e törttel egyenértékű tört $\dpi{120} \frac{2}{4}$ , még kisebb feltételekkel?

igen, a tört $\dpi{120} \frac{1}{2}$ törtnek felel meg $\dpi{120} \frac{2}{4}$ , hiszen a pizza felét is képviseli, ha csak két részre osztjuk.

Tehát ez a három tört egyenértékű: $\dpi{120} \frac{4}{8} \frac{2}{4}\frac{1}{2}$ 2. kérdés: Van-e törttel egyenértékű tört $\dpi{120} \frac{1}{2}$ , még kisebb feltételekkel?

Nem, ezek a lehető legkisebb értékek, vagyis ezt a törtet már nem tudjuk egyszerűsíteni.

Ebben az esetben azt mondjuk, hogy a tört $\dpi{120} \frac{1}{2}$ és a redukálhatatlan forma a töredékből $\dpi{120} \frac{4}{8}$ .

A torta kialakítása megkönnyítette a kisebb kifejezésekkel egyenértékű törtek megtalálását, amelyek a torta felét képviselik.

Most pedig lássunk egy praktikus és egyszerű módszert a törtek egyszerűsítésére anélkül, hogy szemléltető képre lenne szükség.

Hogyan egyszerűsítsünk egy törtet?

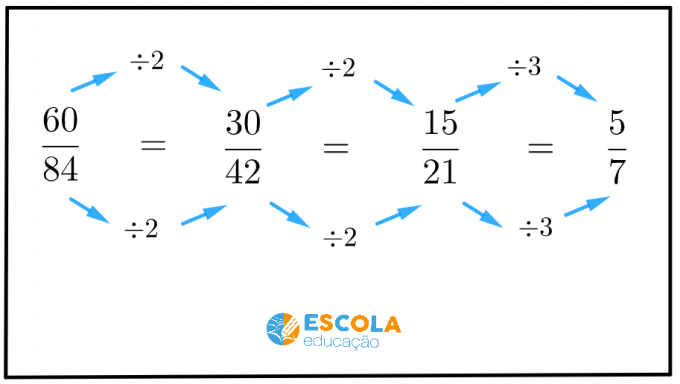
A tört egyszerűsítéséhez osszuk el a tört számlálóját és nevezőjét a-val ugyanaz a szám nagyobb mint 1.

1. példa: Egyszerűsítsük a törtet $\dpi{120} \frac{3}{12}$ .

Az 1-nél nagyobb első szám a 2. Ennek a törtnek mindkét tagja osztható 2-vel?

3 nem osztható 2-vel, mivel az osztás maradéka nem nulla;
A 12 osztható 2-vel, mivel az osztás maradéka nulla.

A két számnak oszthatónak kell lennie! Ha mindkettő nem, menjünk a következő számra.

A következő szám a 3. Ennek a törtnek mindkét tagja osztható 3-mal?

3 osztható 2-vel, mert az osztás maradéka nulla;
A 12 osztható 3-mal, mert az osztás maradéka nulla.

Tehát a tört egyszerűsítése érdekében osszuk el a számlálót és a nevezőt 3-mal.

Ezért muszáj $\dpi{120} \frac{3}{12}\frac{1}{4}$ .

Kérdés: Lehetőség van a tört egyszerűsítésére $\dpi{120} \frac{1}{4}$ ? Nem, ezek ennek a törtnek a lehető legkisebb tagjai.

Akkor, $\dpi{120} \frac{1}{4}$ a tört irreducibilis formája $\dpi{120} \frac{3}{12}$ .

2. példa:Egyszerűsítsük a törtet $\dpi{120} \frac{45}{120}$ .

Akkor, $\dpi{120} \frac{45}{120}\frac{3}{8}$ .

3. példa:Egyszerűsítsük a törtet $\dpi{120} \frac{60}{84}$ .

Nekünk kell $\dpi{120} \frac{60}{84}\frac{5}{7}$ .

Olvasd el te is:

Tevékenységek törtekkel
Hogyan lehet törteket összeadni és kivonni

A törtek egyszerűsítése - Egyenértékű és redukálhatatlan törtek

Hogyan egyszerűsítsünk egy törtet?

Szövegértelmezés: Alázat

Szövegértelmezés: A kegyetlen herceg

Portugál tevékenység: jelzőhangú igék