Pembagian bilangan desimal

click fraud protection

Dalam banyak situasi kita perlu memecahkan akun divisi dengan angka desimal. Misalnya, jika empat pena berharga R$11,20, berapakah harga setiap pena?

Untuk menemukan jawabannya, kita harus membagi angka dalam bentuk desimal dengan bilangan asli: $\dpi{120} \bg_putih 11.20 \div 4 2.8$ . Jadi, setiap pena berharga R$2,80.

Tetapi bagaimana kita sampai pada jawaban ini? Jika Anda masih belum tahu atau memiliki pertanyaan tentang cara mengatasi akun seperti ini, Anda berada di tempat yang tepat! Pada postingan kali ini kami akan mengajarkan cara membagi bilangan desimal.

Contoh 1: Bagilah angka 235,7 dengan 10, dengan 100, dan dengan 1000.

$\dpi{120} \bg_putih 235.7 \div 10 23.57$
$\dpi{120} \bg_putih 235.7 \div 100 2.357$
$\dpi{120} \bg_putih 235,7 \div 1000 0,2357$

Contoh 2: Bagilah angka 1,96 dengan 10, dengan 100, dan dengan 1000.

$\dpi{120} \bg_putih 1,96 \div 10 0,196$
$\dpi{120} \bg_putih 1,96 \div 100 0,0196$
$\dpi{120} \bg_putih 1,96 \div 1000 0,00196$

Aturan ini dapat digeneralisasikan ke nilai selain 10, 100 dan 1000. Jika, misalnya, Anda ingin membagi angka desimal dengan 1.000.000, yaitu angka dengan 6 digit sama dengan 0, cukup pindahkan koma desimal enam angka ke kiri.

Divisi dari bilangan desimal ke bilangan asli

Pertama, ingatlah bahwa setiap angka desimal memiliki bagian bilangan bulat, yang dibentuk oleh satuan (U), puluhan (D), ratusan (C) dst., dan bagian desimal yang dibentuk oleh sepersepuluh (d), seperseratus (c), seperseribu (m) dll.

instagram story viewer

Karena itu, mari kita lihat contoh cara membagi bilangan desimal dengan bilangan asli apa pun.

Contoh: Menghitung $\dpi{120} \bg_putih 8.25 \div 5$

8 unit dibagi 5 menghasilkan 1 unit, dan itu tersisa 3 unit.
3 satuan = 30 persepuluh.
30 persepuluhan + 2 persepuluhan (↓ turun) = 32 persepuluhan.
32 persepuluh dibagi 5 adalah 6, dan itu tersisa 2 sepersepuluh.
Kami menempatkan koma antara 1 dan 6.
2 sepersepuluh = 20 perseratus.
20 sen + 5 sen (↓ turun) = 25 sen.
25 sen dibagi 5 adalah 5 sen dan tidak ada yang tersisa.

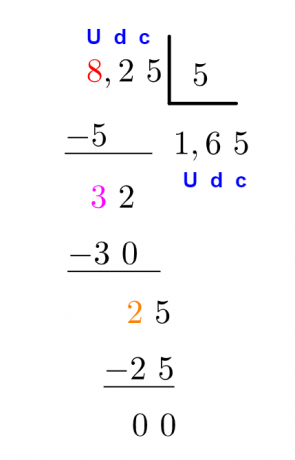
Ada metode alternatif untuk menyelesaikan akun yang sama ini. apa yang kita lakukan adalah hapus koma dan kemudian selesaikan akun pembagian antara bilangan asli.

Untuk menghapus koma:

Kami mengalikan dengan 10 jika angka tersebut memiliki tempat setelah titik desimal;
Kami mengalikan dengan 100 jika angka tersebut memiliki dua tempat setelah titik desimal;
Kami mengalikan dengan 1000 jika angka tersebut memiliki tiga tempat setelah titik desimal;

Dan seterusnya.

Karena 8,25 memiliki dua tempat setelah titik desimal, kita kalikan dengan 100:

$\dpi{120} \bg_putih 8,25 \times 100 825$

Meskipun angka 5 tidak memiliki koma, kita juga harus mengalikannya dengan 100. Kami akan selalu mengalikan dua nomor akun, dividen dan pembagi, dengan angka yang sama.

$\dpi{120} \bg_putih 5 \kali 100 500$

Jadi selesaikan $\dpi{120} \bg_putih 8.25 \div 5$ sama dengan memecahkan $\dpi{120} \bg_putih 825 \div 500$ , yaitu untuk menyelesaikan pembagian antara bilangan asli.

Divisi dari bilangan desimal ke bilangan desimal

Untuk membagi bilangan desimal dengan bilangan desimal lainnya, kita akan mengadopsi prosedur mengubah akun menjadi pembagian bilangan asli, menghilangkan koma.

Untuk menghapus koma:

Kami mengalikan dengan 10 jika angka tersebut memiliki tempat setelah titik desimal;
Kami mengalikan dengan 100 jika angka tersebut memiliki dua tempat setelah titik desimal;
Kami mengalikan dengan 1000 jika angka tersebut memiliki tiga tempat setelah titik desimal;

Dan seterusnya.

Contoh 1: Hitung $\dpi{120} \bg_putih 2.7 \div 0.9$ .

$\dpi{120} \bg_putih 2,7 \times 10 27$
$\dpi{120} \bg_putih 0,9 \times 10 9$

Kemudian, $\dpi{120} \bg_putih 2.7 \div 0.9 27 \div 9 3$ .

Contoh 2: Hitung $\dpi{120} \bg_putih 0,8 \div 0,02$ .

$\dpi{120} \bg_putih 0,8 \kali 100 80$
$\dpi{120} \bg_putih 0,02 \times 100 2$

Perhatikan bahwa meskipun angka 0,8 hanya memiliki satu tempat setelah titik desimal, kita mengalikannya dengan 100. Hal ini kami lakukan karena angka 0,02 perlu dikalikan dengan 100 dan kedua nomor rekening tersebut harus dikalikan dengan angka yang sama.

Dengan demikian, $\dpi{120} \bg_putih 0,8 \div 0,02 80 \div 2 40$ .

Lihat juga:

Divisi
algoritma pembagian

Siapa orang barbar itu? Sejarah, Makna, Bangsa Barbar

on Aug 03, 2023

Pembagian bilangan desimal

Divisi dari bilangan desimal ke bilangan asli

Divisi dari bilangan desimal ke bilangan desimal

Pengumuman Enem 2018 diterbitkan: lihat apa yang baru untuk tahun ini

Program Dialog Positif, melibatkan, mengajarkan dan mengubah hubungan antara orang tua dan anak serta pendidik dan siswa

Siapa orang barbar itu? Sejarah, Makna, Bangsa Barbar