როგორ გავამარტივოთ წილადები - ეკვივალენტური და შეუქცევადი წილადები

Რას ნიშნავს წილადის გამარტივება? წილადის გამარტივება ნიშნავს ეკვივალენტური წილადის დაწერას, რომელსაც აქვს უფრო მცირე მრიცხველი და მნიშვნელი, ვიდრე თავდაპირველი წილადი.

ტოლფასი წილადები სხვა არაფერია თუ არა წილადები, რომლებიც წარმოადგენენ ერთსა და იმავე რაოდენობას ან მთლიანის ნაწილს.

მეტის ნახვა

რიო-დე-ჟანეიროს სტუდენტები ოლიმპიურ თამაშებზე მედლებისთვის იბრძოლებენ...

მათემატიკის ინსტიტუტი ღიაა ოლიმპიადაზე რეგისტრაციისთვის…

იმის გასაგებად, თუ როგორ მუშაობს ეს, განიხილეთ შემდეგი მაგალითი:

8 ცალი პიცაში პიცის ნახევარს წარმოადგენს ფრაქცია $\dpi{120} \frac{4}{8}$ . თუმცა, თუ იგივე პიცა იყოფა მხოლოდ 4 ნაწილად, მისი ნახევარი წარმოდგენილია წილადით $\dpi{120} \frac{2}{4}$ . იხილეთ ფიგურა ქვემოთ: ტოლფასი წილადები

მიუხედავად იმისა, რომ აქვს განსხვავებული მრიცხველი და მნიშვნელი, წილადები $\dpi{120} \frac{4}{8}$ Ეს არის $\dpi{120} \frac{2}{4}$ წარმოადგენს იგივე რაოდენობის პიცას. ამრიგად, ეს წილადები ექვივალენტურია, რაც ნიშნავს:

$\dpi{120} \frac{4}{8} \frac{2}{4}$

Კითხვა 1: არის თუ არა წილადის ტოლფასი წილადი $\dpi{120} \frac{2}{4}$ , კიდევ უფრო მცირე პირობებით?

დიახ, ფრაქცია $\dpi{120} \frac{1}{2}$ წილადის ტოლია $\dpi{120} \frac{2}{4}$ , რადგან ის ასევე წარმოადგენს პიცის ნახევარს, როდესაც ის იყოფა მხოლოდ ორ ნაწილად.

ასე რომ, ეს სამი წილადი ტოლია:

$\dpi{120} \frac{4}{8} \frac{2}{4}\frac{1}{2}$ კითხვა 2: არის თუ არა წილადის ტოლფასი წილადი $\dpi{120} \frac{1}{2}$ , კიდევ უფრო მცირე პირობებით?

არა, ეს არის უმცირესი შესაძლო მნიშვნელობები, ანუ ამ წილადის გამარტივება აღარ შეგვიძლია.

ამ შემთხვევაში ვამბობთ, რომ წილადი $\dpi{120} \frac{1}{2}$ და შეუქცევადი ფორმა წილადის $\dpi{120} \frac{4}{8}$ .

ტორტის დიზაინმა გაადვილა ეკვივალენტური წილადების პოვნა უფრო მცირე ტერმინებით, რათა წარმოადგენდეს ტორტის ნახევარს.

ახლა ვნახოთ წილადების გამარტივების პრაქტიკული და მარტივი გზა საილუსტრაციო გამოსახულების დახმარების გარეშე.

როგორ გავამარტივოთ წილადი?

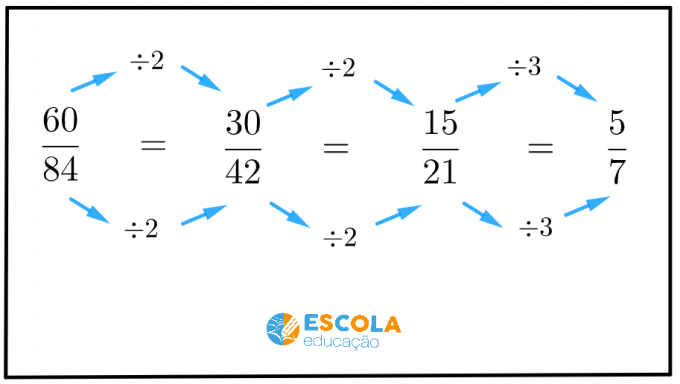
წილადის გასამარტივებლად, გაყავით წილადის მრიცხველი და მნიშვნელი იგივე ნომერი 1-ზე მეტი.

მაგალითი 1: გავამარტივოთ წილადი $\dpi{120} \frac{3}{12}$ .

პირველი რიცხვი, რომელიც 1-ზე მეტია, არის ნომერი 2. იყოფა თუ არა ამ წილადის ორივე წევრი 2-ზე?

3 არ იყოფა 2-ზე, რადგან გაყოფის დარჩენილი ნაწილი არ არის ნული;
12 იყოფა 2-ზე, რადგან გაყოფის დარჩენილი ნაწილი არის ნული.

ეს ორი რიცხვი უნდა იყოს გაყოფილი! თუ ორივე არაა, გადავიდეთ შემდეგ ნომერზე.

შემდეგი ნომერი არის 3. იყოფა თუ არა ამ წილადის ორივე წევრი 3-ზე?

3 იყოფა 2-ზე, რადგან გაყოფის დარჩენილი ნაწილი არის ნული;
12 იყოფა 3-ზე, რადგან გაყოფის დარჩენილი ნაწილი არის ნული.

ასე რომ, წილადის გასამარტივებლად, მრიცხველი და მნიშვნელი გავყოთ 3-ზე.

აქედან გამომდინარე, ჩვენ უნდა $\dpi{120} \frac{3}{12}\frac{1}{4}$ .

Კითხვა: შესაძლებელია წილადის გამარტივება $\dpi{120} \frac{1}{4}$ ? არა, ეს არის ამ წილადის უმცირესი შესაძლო ტერმინები.

მაშინ, $\dpi{120} \frac{1}{4}$ არის წილადის შეუქცევადი ფორმა $\dpi{120} \frac{3}{12}$ .

მაგალითი 2:გავამარტივოთ წილადი $\dpi{120} \frac{45}{120}$ .

მაშინ, $\dpi{120} \frac{45}{120}\frac{3}{8}$ .

მაგალითი 3:გავამარტივოთ წილადი $\dpi{120} \frac{60}{84}$ .

Ჩვენ უნდა $\dpi{120} \frac{60}{84}\frac{5}{7}$ .

წაიკითხეთ ასევე:

მოქმედებები წილადებით
როგორ დავამატოთ და გამოვაკლოთ წილადები

პორტუგალიური აქტივობა: წარსული სრულყოფილი

როგორ გავამარტივოთ წილადები - ეკვივალენტური და შეუქცევადი წილადები

როგორ გავამარტივოთ წილადი?

პორტუგალიური აქტივობა: წარსული სრულყოფილი

პორტუგალიური აქტივობა: ზმნები აწმყო დროში

ისტორიის აქტივობა: სპარტა, გამაგრებული სახელმწიფო