Kad mēs veidojam kontus reizināšanaar cipariem, kuriem ir vairāk nekā divi cipari, parasti atstāj vienu vai vairākas tukšas vietas.
Bet vai jūs zināt, kāpēc mēs atstājam šīs vietas tukšas? Vai tie ir neaizstājami? Vai jūs varat veikt reizināšana bez tukšām atstarpēm?
redzēt vairāk
Studenti no Riodežaneiro cīnīsies par medaļām olimpiskajās spēlēs…
Matemātikas institūts ir atvērts reģistrācijai olimpiādei…
Lasiet tālāk, lai uzzinātu atbildes uz visiem šiem jautājumiem!
Paskaidrosim ar piemēru.
Aprēķiniet 11x12
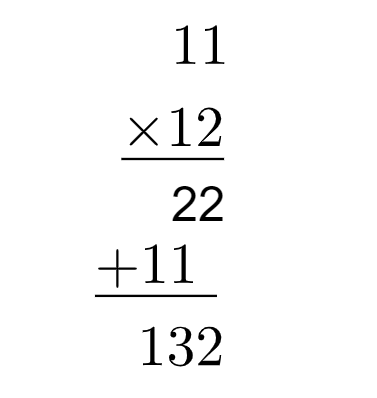
Mēs reizinām 11 ar 2 un pēc tam reizinām 11 ar 1.
11 x 2 = 22 → mēs to rakstām zem domuzīmes.
11 x 1 = 11 → mēs rakstām zem iepriekšējā rezultāta, atstājot atstarpi labajā pusē.
Visbeidzot, mēs pievienojam, iegūstot vērtību 132.
Bet kāpēc mēs atstājam šo vietu? Mēs atstājam vietu, lai praktiski iegūtu pareizo atbildi!
Ņemiet vērā, ka 12 = 10 + 2 → viens desmit plus divi vieni.
Tātad, reizināt 11 ar 12 ir tas pats, kas atsevišķi reizināt 11 ar 10 un 11 ar 2 un saskaitīt rezultātus.
11 x 10 = 110
11 x 2 = 22
Saskaitot šos rezultātus: 110 + 22 = 132. Tāpēc 11 x 22 = 132.
Praktiskajā metodē šo rezultātu iegūst tikai ar vietu. Pretējā gadījumā mēs iegūtu 33, un tas būtu nepareizi, jo mēs jau redzējām, ka 132 ir pareizi.
Ja tukšās atstarpes jūs mulsina, veicot reizināšanas summu, ziniet, ka no tā var izvairīties, katrā atstarpē vienkārši pievienojot nulli.
Tas darbojas, jo patiesībā katra atstarpe faktiski atbilst nullei, mēs to jau redzējām, kad pirms reizināšanas veicām skaitļa 12 sadalīšanu.
Tātad jūsu konts, kuram pievienota nulle, būs pareizs:

Jūs varētu arī interesēt: