Enkele thema's van wiskunde worden altijd afgerekend Nationaal middelbare schoolexamen (En ook). Hoewel de toets divers is, op basis van eerdere examens, is het mogelijk om inhoud op te merken die altijd aan bod komt.
Als je niet weet waar je moet beginnen met studeren of als je wilt controleren of je op de goede weg bent, dan is dit bericht iets voor jou, omdat we de inhoud hebben vermeld die heel vaak in de test valt.
Bekijk meer
Jongeren verliezen interesse in de Enem, zeggen experts;...
Studenten uit Rio de Janeiro strijden om medailles op de Olympische Spelen...
Bekijk hieronder enkele van de wiskundige onderwerpen die je moet kennen voor het vijand.
Bekijk onderwerpen om te bestuderen en maak meer kans om goed te presteren in de Enem-wiskundetest.
In veel Enem-vragen kun je informatie vinden die is uitgedrukt in fractionele, decimale of procentuele vorm.
Daarom is deze inhoud eenvoudig en erg belangrijk voor degenen die willen slagen in de test. U moet weten hoe u op deze drie verschillende manieren met getallen omgaat, ertussen kunt converteren en bewerkingen kunt uitvoeren.
Als u vragen of problemen heeft met fracties, raden we aan de volgende teksten te lezen:
Om meer over te weten decimale getallen, hoe je rekent met getallen met een komma, zie:
Als je problemen hebt met procenten, controleer de tekst: Hoe percentage berekenen?
Hoeveelheden, verhoudingen en verhoudingen het zijn ook inhouden die erg aanwezig zijn in de Enem-test, het zijn thema's die kunnen worden toegepast op verschillende alledaagse problemen.
Hoeveelheden kunnen onder andere tijd, kosten, gewicht, lengte, snelheid, temperatuur zijn. In veel situaties zijn hoeveelheden direct of omgekeerd gerelateerd. Om het onderscheid tussen de soorten grootheden te begrijpen, leest u: Magnitudes direct en omgekeerd evenredig.
Daarnaast wijdt u zich aan de studie van verhoudingen en proporties. Problemen die ingewikkeld lijken, worden vaak alleen opgelost vanuit deze twee concepten en het gebruik van hun eigenschappen.
Zie ook: Oefeningen op ratio en proportie
Regel van drie kan enkelvoudig of samengesteld zijn. In Enem is het meest basale geval, de regel van drie eenvoudige, wat het meest neigt te vallen.
Het is een eenvoudige procedure, maar veel mensen hebben de neiging om fouten te maken met betrekking tot grootheden. Als de grootheden recht evenredig zijn, is de manier om te berekenen één. Maar als de grootheden omgekeerd evenredig zijn, is de vorm anders.
Bekijk de verschillende manieren om regel van drie simpel en hoe te berekenen door a aan te vinken lijst met regel van drie oefeningen dat we hebben voorbereid.
Om te weten over de samengestelde drie regel, Look: Oefeningen op de regel van drie verbindingen.
In de Enem-test zijn er altijd vragen met vergelijkingen en functies. De eerste stap is om te weten dat vergelijkingen en functies gerelateerd zijn, maar dat ze niet hetzelfde zijn.
Mocht je hierover twijfelen, lees dan: Verschillen tussen functie en vergelijking.
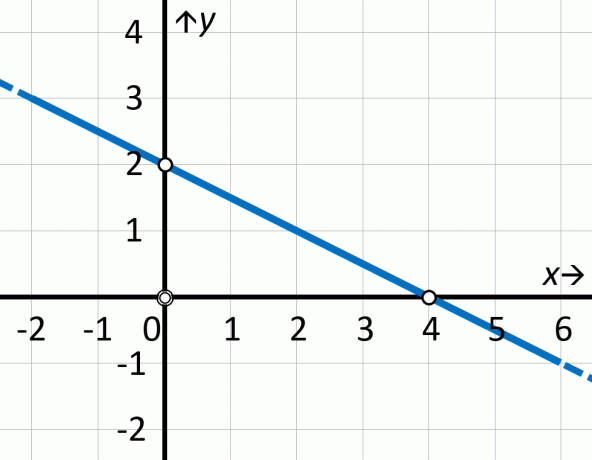
1e graads vergelijking Het is 2e graads vergelijking zijn het meest belast. In het tweede geval moet u weten hoe u de discriminerend en gebruik de Bhaskara's formule.
Zie ook:
A 1e graads functie en de 2e graads functie Ze vallen ook veel op de test. Naast deze is het belangrijk om andere functies te kennen, zoals:
vragen van waarschijnlijkheidHet is en statistieken komen veel voor in de Enem.
Van de kant vanwaarschijnlijkheid, moet u de basis kennen: willekeurig experiment, gebeurtenis, steekproefruimte, waarschijnlijkheidsformule.
Daarnaast is het belangrijk om er een beetje vanaf te weten set theorie, weet hoe je de waarschijnlijkheid van vereniging, snijpunt en voorwaardelijke waarschijnlijkheid.
Combinatorische analyse, arrangementen en combinaties, zijn ook inhoud aanwezig in de test. Deze zaken zijn het waard om in de gaten te houden!
In statistiek, oefen veel de interpretatie van afbeeldingen en de analyse van gegevens gegroepeerd in reeksen. De Enem-test zit vol met afbeeldingen en tabellen!
Zie ook het berekenen en interpreteren van de maatregelen van centraliteit en de verspreidingsmaatregelen.
Gebieden en volumes zijn thema's van vlakke geometrie Het is ruimtelijke geometrie, respectievelijk.
Zie de belangrijkste formules en hoe u de vlak figuur gebied vaker:
Bekijk ook de belangrijkste formules en hoe u het volume van kunt berekenen Geometrische lichamen gewoon:
Mogelijk bent u ook geïnteresseerd:
![ACTIVITEITEN MET COMPLEXE LETTERGRONDEN [MET UITLEG]](/f/06be2f90f9ee03ca8b975982adb0e0dd.jpg?width=100&height=100)
