Divisjon av desimaltall

click fraud protection

I mange situasjoner må vi løse divisjonsregnskap med desimaltall. For eksempel, hvis fire penner koster 11,20 R$, hva er prisen på hver penn?

For å finne svaret må vi dele et tall i desimalform med et naturlig tall: $\dpi{120} \bg_white 11.20 \div 4 2.8$ . Så hver penn koster R$2,80.

Men hvordan kom vi frem til dette svaret? Hvis du fortsatt ikke vet eller har spørsmål om hvordan du løser kontoer som dette, er du på rett sted! I dette innlegget skal vi undervise hvordan dele desimaltall.

Eksempel 1: Del tallet 235,7 med 10, med 100 og med 1000.

$\dpi{120} \bg_white 235.7 \div 10 23.57$
$\dpi{120} \bg_white 235.7 \div 100 2.357$
$\dpi{120} \bg_white 235,7 \div 1000 0,2357$

Eksempel 2: Del tallet 1,96 med 10, med 100 og med 1000.

$\dpi{120} \bg_white 1,96 \div 10 0,196$
$\dpi{120} \bg_white 1,96 \div 100 0,0196$
$\dpi{120} \bg_white 1,96 \div 1000 0,00196$

Denne regelen kan generaliseres til andre verdier enn 10, 100 og 1000. Hvis du for eksempel vil dele et desimaltall med 1 000 000, som er et tall med 6 sifre lik 0, flytter du bare desimaltegnet seks plasser til venstre.

Inndeling fra et desimaltall til et naturlig tall

Først, la oss huske at hvert desimaltall har en heltallsdel, dannet av enheter (U), tiere (D), hundredeler (C) osv., og en desimal del dannet av tideler (d), hundredeler (c), tusendeler (m) osv.

instagram story viewer

Når det er sagt, la oss se et eksempel på hvordan du deler et desimaltall med et hvilket som helst naturlig tall.

Eksempel: Regn ut $\dpi{120} \bg_white 8.25 \div 5$

8 enheter delt på 5 gir 1 enhet, og det er til overs 3 enheter.
3 enheter = 30 tideler.
30 tideler + 2 tideler (↓ går ned) = 32 tideler.
32 tideler delt på 5 er 6, og det er til overs 2 tideler.
Vi setter kommaet mellom 1 og 6.
2 tideler = 20 hundredeler.
20 cent + 5 cent (↓ går ned) = 25 cent.
25 øre delt på 5 er 5 øre og ingenting er til overs.

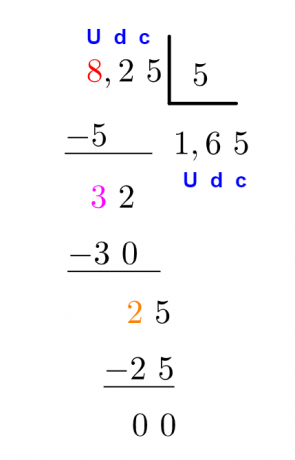
Det er en alternativ metode for å løse denne samme kontoen. det vi gjør er slett kommaet og løs deretter divisjonskontoen mellom naturlige tall.

Slik sletter du kommaet:

Vi multipliserer med 10 hvis tallet har en plass etter desimaltegn;
Vi multipliserer med 100 hvis tallet har to plasser etter desimaltegn;
Vi multipliserer med 1000 hvis tallet har tre plasser etter desimaltegn;

Og så videre.

Siden 8,25 har to plasser etter desimaltegnet, multipliserer vi med 100:

$\dpi{120} \bg_white 8,25 \times 100 825$

Selv om tallet 5 ikke har komma, må vi også gange det med 100. Vi vil alltid gange de to kontonumrene, utbytte og divisor, med samme tall.

$\dpi{120} \bg_white 5 \times 100 500$

Så løs $\dpi{120} \bg_white 8.25 \div 5$ er det samme som å løse $\dpi{120} \bg_white 825 \div 500$ , altså å løse et skille mellom naturlige tall.

Inndeling fra et desimaltall til et desimaltall

For å dele et desimaltall med et annet desimaltall, vil vi bruke prosedyren for å transformere kontoen til naturlig talldivisjon, og eliminere kommaene.

Slik sletter du kommaet:

Vi multipliserer med 10 hvis tallet har en plass etter desimaltegn;
Vi multipliserer med 100 hvis tallet har to plasser etter desimaltegn;
Vi multipliserer med 1000 hvis tallet har tre plasser etter desimaltegn;

Og så videre.

Eksempel 1: Regn ut $\dpi{120} \bg_white 2.7 \div 0.9$ .

$\dpi{120} \bg_white 2.7 \times 10 27$
$\dpi{120} \bg_white 0,9 \times 10 9$

Deretter, $\dpi{120} \bg_white 2.7 \div 0.9 27 \div 9 3$ .

Eksempel 2: Regn ut $\dpi{120} \bg_white 0,8 \div 0,02$ .

$\dpi{120} \bg_white 0,8 \times 100 80$
$\dpi{120} \bg_white 0,02 \times 100 2$

Legg merke til at selv om tallet 0,8 bare har ett sted etter desimaltegn, multipliserer vi det med 100. Vi gjorde dette fordi tallet 0,02 må multipliseres med 100 og de to kontonumrene må multipliseres med samme tall.

Dermed, $\dpi{120} \bg_white 0,8 \div 0,02 80 \div 2 40$ .