Dzielenie liczb dziesiętnych

Przykład 1: Podziel liczbę 235,7 przez 10, 100 i 1000.

• 
• 
• 

Przykład 2: Podziel liczbę 1,96 przez 10, 100 i 1000.

• 
• 
• 

Regułę tę można uogólnić na wartości inne niż 10, 100 i 1000. Jeśli na przykład chcesz podzielić liczbę dziesiętną przez 1 000 000, czyli liczbę z 6 cyframi równymi 0, po prostu przesuń przecinek o sześć miejsc w lewo.

Dział od liczby dziesiętnej do liczby naturalnej

Najpierw pamiętajmy, że każda liczba dziesiętna ma część całkowitą, utworzoną z jednostek (U), dziesiątki (D), setki (C) itd. oraz część dziesiętna utworzona z części dziesiątych (d), części setnych (c), części tysięcznych (m) itd.

To powiedziawszy, zobaczmy przykład dzielenia liczby dziesiętnej przez dowolną liczbę naturalną.

Przykład: Oblicz 

• 8 jednostki podzielone przez 5 dają 1 jednostkę i to zostaje 3 jednostki.
• 3 jednostki = 30 dziesiątych.
• 30 dziesiątych + 2 dziesiąte (↓ w dół) = 32 dziesiąte.
• 32 dziesiąte podzielone przez 5 daje 6 i to zostaje 2 dziesiątki.
• Między 1 a 6 stawiamy przecinek.
• 2 dziesiąte = 20 setnych.
• 20 centów + 5 centów (↓ spada) = 25 centów.
• 25 centów podzielone przez 5 to 5 centów i nic nie zostaje.

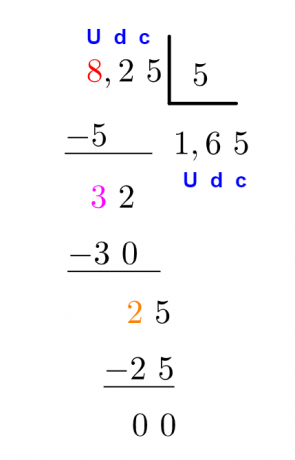
Istnieje alternatywna metoda rozwiązania tego samego konta. co robimy jest usuń przecinek a następnie rozwiąż konto dzielenia między liczbami naturalnymi.

Aby usunąć przecinek:

• Mnożymy przez 10, jeśli liczba ma miejsce po przecinku;
• Mnożymy przez 100, jeśli liczba ma dwa miejsca po przecinku;
• Mnożymy przez 1000, jeśli liczba ma trzy miejsca po przecinku;

I tak dalej.

Ponieważ 8,25 ma dwa miejsca po przecinku, mnożymy przez 100:

Chociaż liczba 5 nie ma przecinka, musimy ją również pomnożyć przez 100. Zawsze będziemy mnożyć dwa numery kont, dywidendę i dzielnik, przez tę samą liczbę.

Więc rozwiąż jest tym samym co rozwiązywanie , czyli rozwiązać dzielenie między liczbami naturalnymi.

Dział od liczby dziesiętnej do liczby dziesiętnej

Aby podzielić liczbę dziesiętną przez inną liczbę dziesiętną, przyjmiemy procedurę przekształcania rachunku na dzielenie liczb naturalnych, eliminując przecinki.

Aby usunąć przecinek:

• Mnożymy przez 10, jeśli liczba ma miejsce po przecinku;
• Mnożymy przez 100, jeśli liczba ma dwa miejsca po przecinku;
• Mnożymy przez 1000, jeśli liczba ma trzy miejsca po przecinku;

I tak dalej.

Przykład 1: Oblicz .

• 
• 

Następnie, .

Przykład 2: Oblicz .

• 
• 

Zauważ, że chociaż liczba 0,8 ma tylko jedno miejsce po przecinku, mnożymy ją przez 100. Zrobiliśmy to, ponieważ liczbę 0,02 należy pomnożyć przez 100, a dwa numery kont należy pomnożyć przez tę samą liczbę.

Zatem, .

Zobacz też:

• Dział
• algorytm dzielenia