O počitek je eden od štirih elementov, ki sestavljajo algoritem deljenja. To je vrednost, ki ostane, da je količnik ena. celo število.
Kadar je ostanek enak nič, pravimo, da je deljenje natančno. V tem primeru je dividenda enaka zmnožku delitelja in količnika:
Poglej več
Dijaki iz Ria de Janeira se bodo na olimpijskih igrah potegovali za medalje...
Inštitut za matematiko je odprt za prijave na olimpijado…
dividenda = delitelj × količnik
Vendar pa obstajajo primeri, ko je preostanek vrednost, ki ni nič. Glej primer:
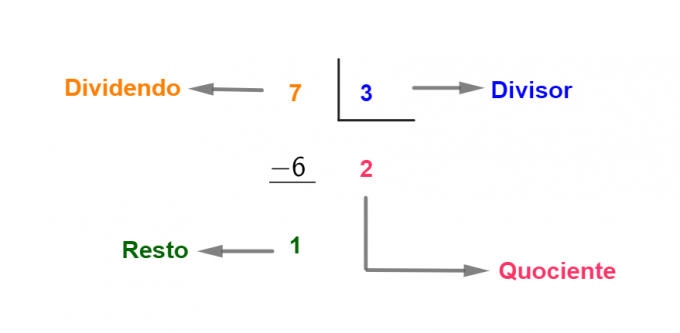
V tem primeru je dividenda enaka zmnožku delitelja in količnika plus ostanek:
dividenda = (deljenec × količnik) + ostanek
Ampak konec koncev, čemu je ostala delitev? Kaj pomeni ta preostala vrednost? Spodaj bomo razložili vse!
Čemu je namenjen ostanek deljenja, bomo razložili z matematičnim problemom, ki bo vključeval dve situacijiveliko različnih.
Videli boste, da čeprav je račun delitve enak pri razrešitvi obeh situacij, bo imel ostanek v vsaki drugačen pomen.
Težava:
Slaščičar proizvaja brigadeiros in jih prodaja v škatlah, ki vsebujejo največ 50 bonbonov.

Predpostavimo, da je na določen dan proizvedla 384 enot.
Situacija 1: Stranka kupi vse neodprte škatle, ki jih ima tisti dan. Zaprte škatle so tiste škatle, ki vsebujejo največje število bonbonov.
Koliko škatel bo prejela ta stranka?
Resolucija:
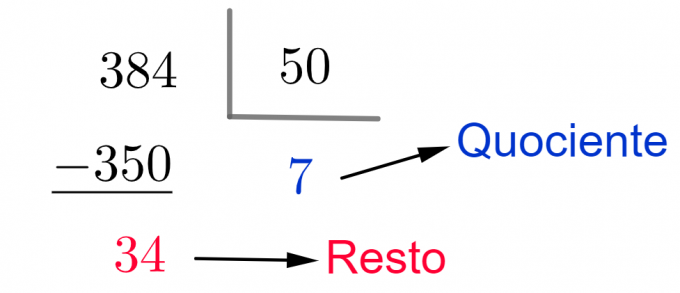
Količnik v tem računu predstavlja število zaključenih zadev. Preostanek označuje količino bonbonov, ki ostanejo pred dokončanjem nove škatle.
Ker želi kupec kupiti samo neodprte škatle, prejme 7 škatel.
Upoštevajte, da preostanek ne vpliva na število škatel, saj preostali bonboni ne bodo prodani tej stranki.
2. situacija: Stranka kupi vse sladkarije, ki jih ima ta dan.
Koliko škatel bo prejela ta stranka?
Resolucija:

V tem primeru bo stranka kupila vse sladkarije, tako da bodo tudi tiste, ki so ostale, dane v škatlo.
Na ta način bo kupec prejel 8 škatel, od tega 7 zaprtih in še eno škatlo s 34 bonboni.
Za razliko od situacije 1 tukaj ostanek posega v število škatel.
Kaj lahko sklepamo iz tega problema?
Preostanek v razdelku bo imel drugačen pomen glede na vsako vrsto problema. V nekaterih primerih se lahko ne upošteva, v drugih pa ne.
Morda vas bo zanimalo tudi: