Hur man förenklar bråk - Ekvivalenta och irreducerbara bråk

Vad det betyder förenkla en bråkdel? Att förenkla ett bråk innebär att skriva ett ekvivalent bråk som har en mindre täljare och nämnare än det ursprungliga bråket.

Ekvivalenta fraktioner är inget annat än bråk som representerar samma mängd eller del av en helhet.

För att förstå hur detta fungerar, överväg följande exempel:

I en 8-delad pizza är bråkdelen som representerar hälften av pizzan . Men om samma pizza är uppdelad i bara 4 bitar, representeras hälften av den av bråkdelen . Se figuren nedan:

Trots att de har olika täljare och nämnare, bråk  Det är  representerar samma mängd pizza. Därför är dessa fraktioner ekvivalenta, vilket betyder att:

Fråga 1: Finns det en bråkdel som motsvarar bråk , med ännu mindre villkor?

ja, bråkdelen  motsvarar bråkdel , eftersom den också representerar hälften av pizzan, när den är uppdelad i bara två delar.

Så dessa tre bråk är ekvivalenta:Fråga 2: Finns det en bråkdel som motsvarar bråk , med ännu mindre villkor?

Nej, det är de minsta möjliga värdena, det vill säga vi kan inte längre förenkla denna bråkdel.

I det här fallet säger vi att bråket  och den oreducerbar form av fraktionen .

Pajdesignen gjorde det enkelt att hitta ekvivalenta bråk med mindre termer för att representera hälften av pajen.

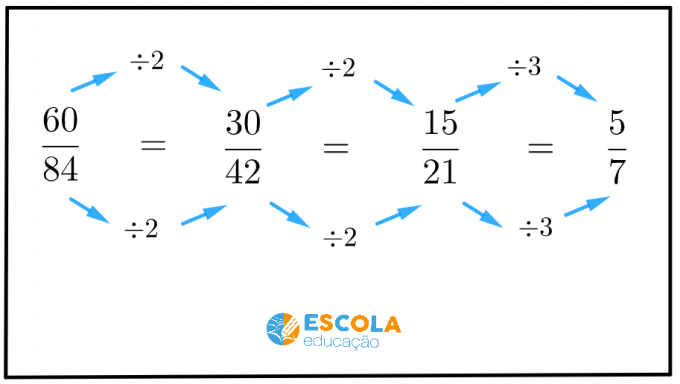
Låt oss nu se ett praktiskt och enkelt sätt att förenkla bråk utan att behöva hjälp av en illustrativ bild.

Hur förenklar man en bråkdel?

För att förenkla ett bråk, dividera bråkets täljare och nämnare med a samma nummer större än 1.

Det första talet större än 1 är talet 2. Är båda termerna i denna bråkdel delbara med 2?

• 3 är inte delbart med 2, eftersom resten av divisionen inte är noll;
• 12 är delbart med 2 eftersom resten av divisionen är noll.

De två talen måste vara delbara! Om båda inte är det, låt oss gå till nästa nummer.

Nästa nummer är 3. Är båda termerna i denna bråkdel delbara med 3?

• 3 är delbart med 2, eftersom resten av divisionen är noll;
• 12 är delbart med 3 eftersom resten av divisionen är noll.

Så, för att förenkla bråket, låt oss dividera täljaren och nämnaren med 3.

Därför måste vi .

Fråga: Det går att förenkla bråket ? Nej, det här är de minsta möjliga termerna av denna bråkdel.

Sedan,  är den irreducerbara formen av fraktionen .

Läs också:

• Aktiviteter med bråk
• Hur man adderar och subtraherar bråk