
Für die Prüfung lernen Nationale Highschool-Prüfung (Und entweder) ist ein wichtiger Schritt für diejenigen, die sich auf offene Studienplätze bewerben möchten. Allerdings ist dieser Studienabschnitt nicht immer so einfach.
Bei Mathematik, Schwierigkeiten bei der schnellen Durchführung von Berechnungen, da der Test umfangreich und die Zeit knapp ist, und beim Auswendiglernen der verschiedenen mathematische Formeln sind einige der Hauptbeschwerden von Studierenden.
Mehr sehen
Studenten aus Rio de Janeiro werden bei den Olympischen Spielen um Medaillen kämpfen…
Das Institut für Mathematik ist offen für die Anmeldung zu den Olympischen Spielen…
Vor diesem Hintergrund haben wir diesen Text mit vorbereitet Mathe-Tipps und Tricks für den Feind für alle, die die Prüfung bestehen wollen!
Wir haben einige wertvolle Tipps für Sie zusammengestellt, die den Enem nehmen werden. Schauen Sie es sich unten an!
Bei Mit 10, 100 und 1000 multiplizieren
Für ganze Zahlen, fügen Sie einfach rechts von der Zahl Nullen hinzu:
56 × 10 = 560
56 × 100 = 5600
56 × 1000 = 56000
Für Dezimal Zahlen, verschieben Sie einfach den Dezimalpunkt entsprechend der Anzahl der Nullen nach rechts:
9,853 × 10 = 98,53
9,853 × 100 = 985,3
9,853 × 1000 = 9853, = 9853
Bei Division durch 10, 100 und 1000 oder jede andere Potenz von 10, es gibt auch einige Strategien, die Sie einem guten Erfolg im Enem näher bringen.
Wenn beide Zahlen auf Null enden, können wir die Nullen streichen, um das Zählen zu erleichtern:
350: 10 = 35: 1 = 35
600: 100 = 6: 1 = 6
29000: 1000 = 29: 1 = 29
Für Dezimal Zahlen, verschieben Sie einfach den Dezimalpunkt entsprechend der Anzahl der Nullen nach links:
256,7: 10 = 25,67
256,7: 100 = 2,567
256,7: 1000 = ,2567 = 0,2567
Um mit Spartenkonten besser vorbereitet zu sein, lesen Sie unseren Text: Tipps und Tricks zur Divisionsberechnung.
A Bhaskaras Formel ist eines der bekanntesten in der Mathematik, wird aber von vielen Oberstufenschülern auch als eines der am schwierigsten auswendig zu merkenden und anzuwendenden angesehen.
Eine Alternative zu Bhaskaras Formel zum Finden der Wurzeln von a Gleichung 2. Grades, und das Summen- und Produktmethode.
Summe (S) und Produkt (P):
S = -b/a und P = c/a
Berechnen Sie S und P aus den Koeffizienten der Gleichung und die Wurzeln sind zwei Zahlen, deren Summe S und deren Produkt P ist.
Beispiel:
x² – 3x – 10
S = -(-3)/1 = 3 und P = -10/1 = -10
Die Wurzeln sind 5 und -2, weil 5. -2 = -10 und 5 + (-2) = 3.
Im Folgenden stellen wir einige Tricks vor, die Ihnen helfen, sich sehr nützliche mathematische Formeln zu merken und sie während des Enem-Tests im Gedächtnis zu behalten.
Sich an die Position erinnern Sinus, Cosinus und Tangens Bei der trigonometrischer Kreis, merken Sie sich einfach den folgenden Reim:
„Sinus im Stehen, Kosinus im Liegen und Tangens auf der Seite.“
Zum trigonometrische Verhältnisse Bei der rechtwinkliges Dreieck Beteiligen Sie die gegenüberliegenden und benachbarten Beine sowie die Hypotenuse. Um nicht durch die drei Formeln verwechselt zu werden, merken Sie sich folgenden Satz:
„Ich rannte und fiel auf Kokain.“
Sinus = co/Hip → ran
Kosinus = Hier/Hip → fallen
Tangente = co/Hier → Cola
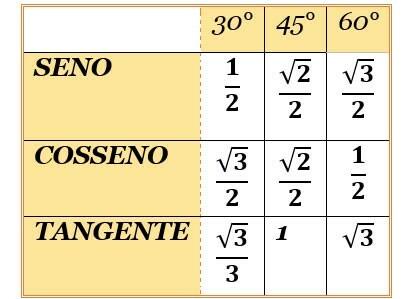
Bemerkenswerte Winkel sind die Winkel 30°, 45° und 60°. Sie werden so genannt, gerade weil sie so verwendet werden. Sie müssen sich also die Werte der Sinus- und Kosinusfunktionen dieser Winkel merken.
Als? Es gibt ein einfaches Lied:
"Eins zwei drei.
Drei zwei eins.
Darunter sind alle zwei.
Wurzel, wo keine ist.“
Wenn Sie sich an dieses Lied erinnern, stellen Sie einfach den Tisch zusammen und es gibt keinen Fehler! Um die Tangenswerte zu ermitteln, dividieren Sie einfach den Sinus durch den Cosinus.
Beginnt um Bogenadditions- und Subtraktionsformelnkönnen viele Geometrieprobleme gelöst werden. Insgesamt gibt es jedoch vier Formeln, die sehr ähnlich sind.
Um nicht verwirrt zu werden, merken Sie sich den folgenden Satz für den Sinus:
Setz dich, kratz! Setz dich, kratz!
Sünde (a + b) = Sünde a. cos b + sin b. weil a
Sin(a – b) = sin a. cos b – sin b. weil a
Nun zum Kosinus:
Jucken, jucken! Setz dich, setz dich!
Kosinus (a + b) = cos a. cos b + sin a. ohne b
Kosinus (a – b) = cos a. cos b – sin a. ohne b
Kombinatorische Analyse fällt im Enem-Test normalerweise stark ab. Daher ist es wichtig, die Formeln zu kennen Anordnung und Kombination, die es ermöglichen, die Anzahl möglicher Cluster zu berechnen, die mit einer Gesamtzahl von Elementen in verschiedenen Situationen gebildet werden können.
Um sich diese Formeln zu merken, können Sie einfach zwei Sätze auswendig lernen. Zur Einordnung lautet der Satz:
"Astill Nzum PKnochen. NEINzum! NEINzum PKnochen!"
Und zur Kombination:
„WFreund Nzum POde. NEINzum! POde! NEINzum POde!"
arithmetische Folge (PA) ist der Sequenztyp, der in Tests am meisten abfällt. Die Formel für den allgemeinen Begriff eines AP kann man sich aus dem folgenden Satz merken:
“Astill Nzum Dervereinbart worden 1Ngeliebte Ric!“
“SIn Ngeliebt? Aarrangieren 1Ngeliebte NEi und teilen für NDu zwei!”
Sie könnten auch interessiert sein:

