O rest is one of the four elements that make up the division algorithm. It is the value left over for the quotient to be one. integer.
When the remainder is equal to zero, we say that the division is exact. In this case, the dividend is equal to the product of the divisor and the quotient:
see more
Students from Rio de Janeiro will compete for medals at the Olympics…
The Institute of Mathematics is open for registration for the Olympics…
dividend = divisor × quotient
However, there are cases where the remainder is a non-zero value. See an example:
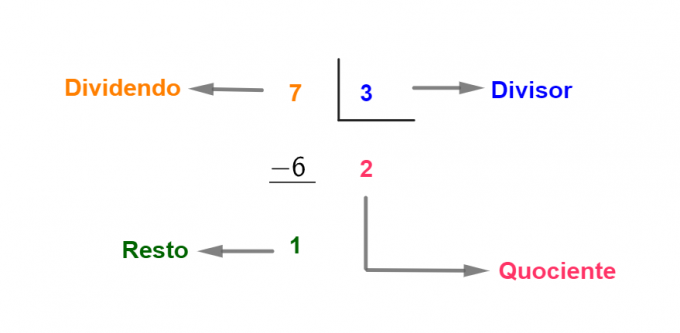
In this case, the dividend is equal to the product of the divisor and the quotient plus the remainder:
dividend = (divisor × quotient) + remainder
But after all, what is the rest of the division for? What does this remaining value mean? We'll explain everything below!
We will explain what the remainder of the division is for through a mathematical problem that will involve two situationsmany different.
You will see that, although the division account is the same in the resolution of the two situations, the remainder will have a different meaning in each one.
Problem:
A confectioner produces brigadeiros and sells them in boxes that hold a maximum of 50 sweets.

Assume that on a certain day she produced 384 units.
Situation 1: A customer buys all the unopened boxes she has that day. Closed boxes are the boxes that contain the maximum number of candies.
How many boxes will this customer receive?
Resolution:
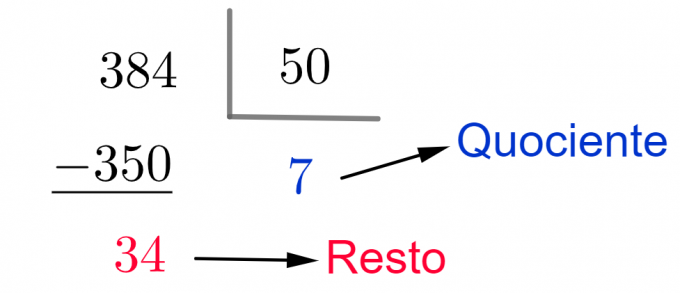
The quotient in this account represents the number of closed boxes. The rest indicates the amount of candies left before completing a new box.
As the customer wants to buy only unopened boxes, he will receive 7 boxes.
Note that the rest does not affect the number of boxes, as the leftover candies will not be sold to this customer.
Situation 2: A customer buys all the sweets she has that day.
How many boxes will this customer receive?
Resolution:

In this situation, the customer will buy all the sweets, so the ones that are left will also be placed in a box.
In this way, the customer will receive 8 boxes, 7 of which are closed and another box with 34 candies.
Unlike situation 1, here the remainder interferes with the number of boxes.
What can we conclude from this problem?
The remainder in a division will have different importance according to each type of problem. In some cases it may be disregarded, in others not.
You may also be interested:

