Close
Menu

Signs of a 2nd degree equation

One 2nd degree function is any function of the form f(x) = ax² + bx + c = 0, with The, B It is w being real numbers and The different from zero.

study the signs of a 2nd degree function means saying for what values ​​of x the function is positive, negative or equal to zero.

see more

Students from Rio de Janeiro will compete for medals at the Olympics…

The Institute of Mathematics is open for registration for the Olympics…

In this way, we need to identify what are the values ​​of x where we have:

f (x) > 0 → positive function

f (x) < 0 → negative function

f (x) = 0 → null function

But how can we know this? One of the ways to study the sign of a 2nd degree function is through its graph, which is a parable.

Signs of a 2nd degree function from the graph

At the cartesian plane, f (x) > 0 corresponds to the part of the parabola that is above the x axis, f (x) = 0 the part of the parabola that intersects the x axis and f (x) < 0, the part of the parabola that is below the x axis .

So we just need to sketch the parabola to identify the signs of the function. The sketch is made simply by knowing what the 

concavity of the parabola and whether or not it intersects the x-axis, and if it does, at what points it does.

We can have six different cases.

Case 1) Signs of a 2nd degree function with two roots \dpi{120} \bg_white \mathrm{x_1} It is \dpi{120} \bg_white \mathrm{x_2} distinct and concavity of the parabola facing upwards.

2nd degree function signs

From the graph, we can identify that:

\dpi{120} \bg_white \left\{\begin{matrix} \mathrm{f (x) 0, if\: \mathrm{x x_1} \: or\: \mathrm{x x_2}} \\ \mathrm{f (x) 0, \: if\: x x_1 \: or \: x x_2}\\ \mathrm{f (x) 0, \: if\: x_1 x x_2} {\color{White} 0000} \end{matrix}\right.

Case 2) Signs of a 2nd degree function with two roots \dpi{120} \bg_white \mathrm{x_1} It is \dpi{120} \bg_white \mathrm{x_2} distinct and concavity of the parabola facing downwards.

Signs of a 2nd degree function

From the graph, we can identify that:

\dpi{120} \bg_white \left\{\begin{matrix} \mathrm{f (x) 0, \: if\: x_1 x x_2} {\color{White} 0000} \\ \mathrm{f (x) 0, \: if\: x x_1 \: or \: x x_2}\\ \mathrm{f (x) 0, if\: \mathrm{x x_1} \: or \: \mathrm{x x_2 }} \end{matrix}\right.

Case 3) Signs of a 2nd degree function with two roots \dpi{120} \bg_white \mathrm{x_1} It is \dpi{120} \bg_white \mathrm{x_2} equal and concavity of the parabola facing upwards.

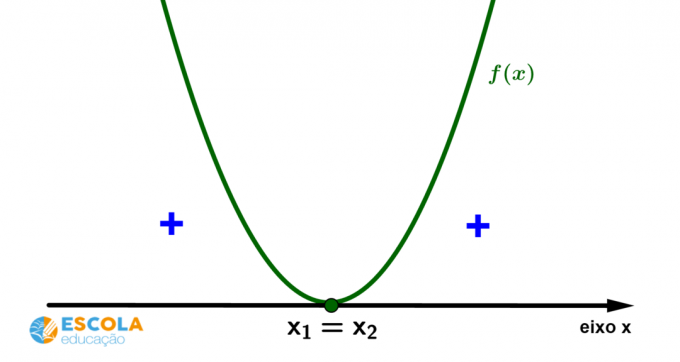
Signs of a 2nd degree function

From the graph, we can identify that:

\dpi{120} \bg_white \left\{\begin{matrix} \mathrm{f (x) 0, \: if\: x x_1}\\ \mathrm{f (x) 0, if\: \mathrm{ x \neq x_1 }} \end{matrix}\right.

Case 4) Signs of a 2nd degree function with two roots \dpi{120} \bg_white \mathrm{x_1} It is \dpi{120} \bg_white \mathrm{x_2} equal and concavity of the parabola facing downwards.

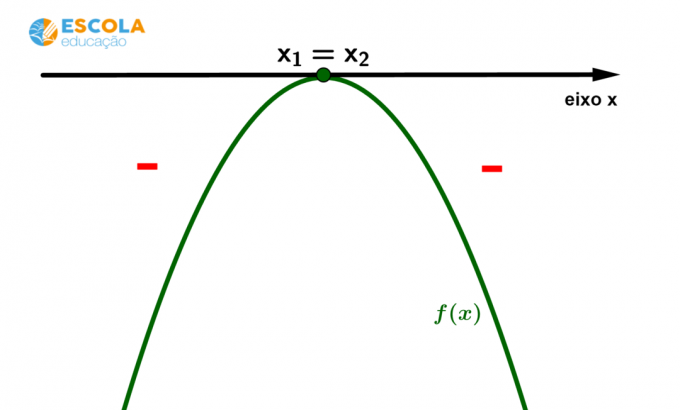
Signs of a 2nd degree function

From the graph, we can identify that:

\dpi{120} \bg_white \left\{\begin{matrix} \mathrm{f (x) 0, \: if\: x x_1}\\ \mathrm{f (x) 0, if\: \mathrm{ x \neq x_1 }} \end{matrix}\right.

Case 5) Signs of a function of the 2nd degree without real roots and parabola concave upwards.Signs of a 2nd degree function

In this case, we have f (x) > 0 for any x belonging to the reals.

Case 6) Signs of a function of the 2nd degree without real roots and concavity of the parabola facing downwards.

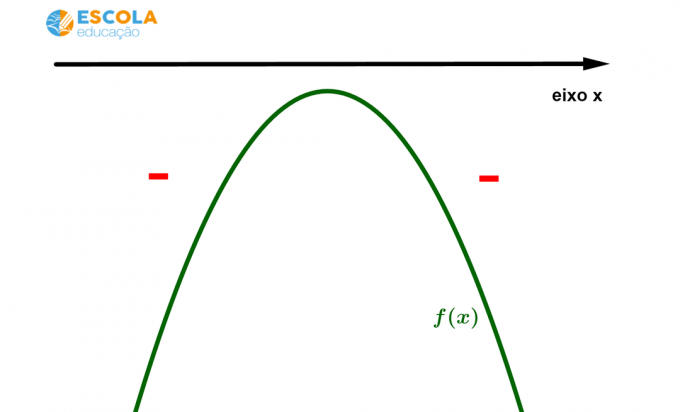
Signs of a 2nd degree function

In this case, we have f (x) < 0 for any x belonging to the reals.

How to check the concavity of the parabola

The concavity of the parabola can be determined by the value of the coefficient The of the function of the 2nd degree.

  • If a > 0, then the parabola is concave upwards;
  • If a < 0, then the parabola is concave downwards.

How to check if the parabola intersects the x-axis

Checking whether or not the parabola intersects the x-axis means determining whether or not the function has roots and, if so, what they are. We can determine this by calculating the discriminating: \dpi{120} \bg_white \Delta b^2 - 4.a.c.

  • if \dpi{120} \bg_white \Delta > 0, the function has two different real roots, and the parabola intersects the x-axis at two different points.
  • if \dpi{120} \bg_white \Delta = 0, the function has two equal real roots, the parabola intersects the x-axis at a single point.
  • if \dpi{120} \bg_white \Delta < 0, the function has no real roots and the parabola does not intersect the x-axis, being entirely above of the x-axis if it is concave upwards and completely below the x-axis if it is concave downwards low.

In the first two cases where there are roots, they can be calculated from the bhaskara's formula.

You may also be interested:

  • How to graph the quadratic function
  • Parabola vertex coordinates
  • First degree function exercises (affine function)
  • Trigonometric Functions – Sine, Cosine and Tangent
1 Year5th YearLiteraturesPortuguese LanguageMind Map FungiMind Map ProteinsMathMaternal IiMatterEnvironmentLabor MarketMythology6 YearMoldsChristmasNewsNews EnemNumericalWords With CParlendasSharing AfricaThinkersLesson Plans6th YearPoliticsPortugueseRecent Posts Previous PostsSpringFirst World WarMain