Comment simplifier des fractions - Fractions équivalentes et irréductibles

Ce que cela veut dire simplifier une fraction? Simplifier une fraction signifie écrire une fraction équivalente qui a un numérateur et un dénominateur plus petits que la fraction originale.

Fractions équivalentes ne sont rien de plus que des fractions qui représentent la même quantité ou une partie d'un tout.

Des étudiants de Rio de Janeiro concourront pour des médailles aux Jeux Olympiques…

L'Institut de Mathématiques est ouvert aux inscriptions pour les Jeux Olympiques…

Pour comprendre comment cela fonctionne, considérons l'exemple suivant :

Dans une pizza de 8 pièces, la fraction représentant la moitié de la pizza est $\dpi{120} \frac{4}{8}$ . Cependant, si cette même pizza est divisée en seulement 4 morceaux, la moitié de celle-ci est représentée par la fraction $\dpi{120} \frac{2}{4}$ . Voir la figure ci-dessous : Fractions équivalentes

Malgré un numérateur et un dénominateur différents, les fractions $\dpi{120} \frac{4}{8}$ C'est $\dpi{120} \frac{2}{4}$ représentent la même quantité de pizza. Par conséquent, ces fractions sont équivalentes, ce qui signifie que :

$\dpi{120} \frac{4}{8} \frac{2}{4}$

Question 1: Existe-t-il une fraction équivalente à la fraction $\dpi{120} \frac{2}{4}$ , avec des termes encore plus petits ?

oui la fraction $\dpi{120} \frac{1}{2}$ est équivalent à la fraction $\dpi{120} \frac{2}{4}$ , car elle représente également la moitié de la pizza, lorsqu'elle est divisée en deux morceaux seulement.

Donc ces trois fractions sont équivalentes : $\dpi{120} \frac{4}{8} \frac{2}{4}\frac{1}{2}$ Question 2: Existe-t-il une fraction équivalente à la fraction $\dpi{120} \frac{1}{2}$ , avec des termes encore plus petits ?

Non, ce sont les plus petites valeurs possibles, c'est-à-dire qu'on ne peut plus simplifier cette fraction.

Dans ce cas, on dit que la fraction $\dpi{120} \frac{1}{2}$ et le forme irréductible de la fraction $\dpi{120} \frac{4}{8}$ .

La conception de la tarte a facilité la recherche de fractions équivalentes avec des termes plus petits pour représenter la moitié de la tarte.

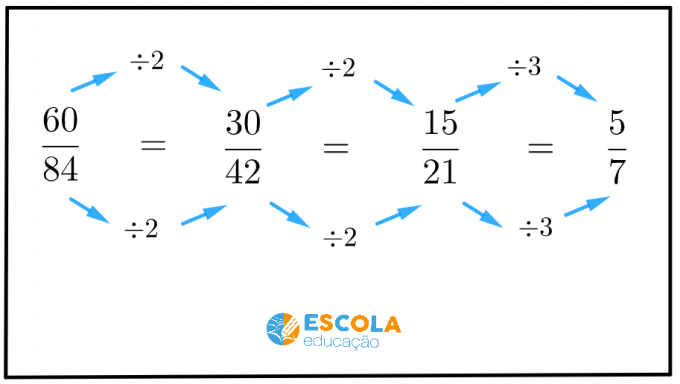
Voyons maintenant un moyen pratique et facile de simplifier des fractions sans avoir besoin de l'aide d'une image illustrative.

Comment simplifier une fraction ?

Pour simplifier une fraction, divisez le numérateur et le dénominateur de la fraction par un même nombre supérieur à 1.

Exemple 1: Simplifions la fraction $\dpi{120} \frac{3}{12}$ .

Le premier nombre supérieur à 1 est le nombre 2. Les deux termes de cette fraction sont-ils divisibles par 2 ?

3 n'est pas divisible par 2, car le reste de la division n'est pas nul ;
12 est divisible par 2 puisque le reste de la division est nul.

Les deux nombres doivent être divisibles! Si les deux ne le sont pas, passons au numéro suivant.

Le nombre suivant est 3. Les deux termes de cette fraction sont-ils divisibles par 3 ?

3 est divisible par 2, car le reste de la division est nul ;
12 est divisible par 3 car le reste de la division est nul.

Donc, pour simplifier la fraction, divisons le numérateur et le dénominateur par 3.

Dès lors, nous devons $\dpi{120} \frac{3}{12}\frac{1}{4}$ .

Question: Il est possible de simplifier la fraction $\dpi{120} \frac{1}{4}$ ? Non, ce sont les plus petits termes possibles de cette fraction.

Alors, $\dpi{120} \frac{1}{4}$ est la forme irréductible de la fraction $\dpi{120} \frac{3}{12}$ .

Exemple 2 :Simplifions la fraction $\dpi{120} \frac{45}{120}$ .

Alors, $\dpi{120} \frac{45}{120}\frac{3}{8}$ .

Exemple 3 :Simplifions la fraction $\dpi{120} \frac{60}{84}$ .

Nous devons $\dpi{120} \frac{60}{84}\frac{5}{7}$ .

A lire aussi:

Activités avec fractions
Comment additionner et soustraire des fractions

Comment simplifier des fractions - Fractions équivalentes et irréductibles

Comment simplifier une fraction ?

Activité de géographie: mondialisation et inégalités

Activité mathématique: situations problématiques

Activité de philosophie: Logique