O odmor je jedan od četiri elementa koji čine algoritam dijeljenja. To je vrijednost koja je preostala da kvocijent bude jedan. cijeli broj.
Kada je ostatak jednak nuli, kažemo da je dijeljenje egzaktno. U ovom slučaju, dividenda je jednaka umnošku djelitelja i količnika:
vidi više
Učenici iz Rio de Janeira borit će se za medalje na Olimpijskim igrama…
Institut za matematiku otvoren je za prijave za Olimpijadu…
dividenda = djelitelj × količnik
Međutim, postoje slučajevi u kojima je ostatak vrijednost različita od nule. Pogledajte primjer:
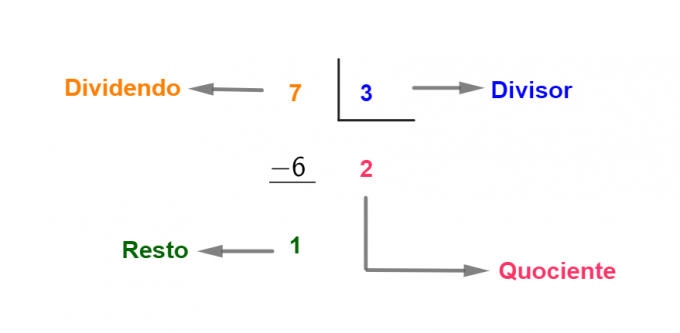
U ovom slučaju, dividenda je jednaka umnošku djelitelja i kvocijenta plus ostatak:
dividenda = (djelitelj × količnik) + ostatak
Ali nakon svega, čemu služi ostatak divizije? Što znači ova preostala vrijednost? Sve ćemo objasniti u nastavku!
Čemu služi ostatak dijeljenja objasnit ćemo kroz matematički problem koji će uključivati dvije situacijemnogo različitih.
Vidjet ćete da, iako je račun dijeljenja isti u razrješenju dviju situacija, ostatak će imati različito značenje u svakoj od njih.
Problem:
Slastičar proizvodi brigadeirose i prodaje ih u kutijama koje sadrže najviše 50 slatkiša.

Pretpostavimo da je određenog dana proizvela 384 jedinice.
Situacija 1: Kupac kupuje sve neotvorene kutije koje ima tog dana. Zatvorene kutije su kutije koje sadrže maksimalan broj bombona.
Koliko će kutija ovaj kupac dobiti?
rezolucija:
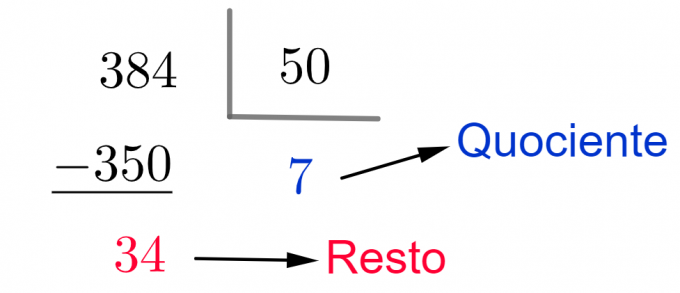
Kvocijent na ovom računu predstavlja broj zaključenih predmeta. Ostatak označava količinu preostalih bombona prije popunjavanja nove kutije.
Kako kupac želi kupiti samo neotvorene kutije, dobit će 7 kutija.
Imajte na umu da ostatak ne utječe na broj kutija, jer preostali bomboni neće biti prodani ovom kupcu.
Situacija 2: Kupac kupi sve slatkiše koje ima tog dana.
Koliko će kutija ovaj kupac dobiti?
rezolucija:

U ovoj situaciji, kupac će kupiti sve slatkiše, pa će i oni koji su preostali biti stavljeni u kutiju.
Na taj način kupac će dobiti 8 kutija od kojih je 7 zatvorenih i još jednu kutiju sa 34 bombona.
Za razliku od situacije 1, ovdje ostatak interferira s brojem kutija.
Što možemo zaključiti iz ovog problema?
Ostatak u dijeljenju imat će različitu važnost prema svakoj vrsti problema. U nekim slučajevima može se zanemariti, u drugima ne.
Možda će vas također zanimati: