Divisione di numeri decimali

In molte situazioni dobbiamo risolvere conti di divisione con numeri decimali. Ad esempio, se quattro penne costano R$ 11,20, qual è il prezzo di ciascuna penna?

Per trovare la risposta dobbiamo dividere un numero in forma decimale per un numero naturale: $\dpi{120} \bg_white 11.20 \div 4 2.8$ . Quindi, ogni penna costa R $ 2,80.

Ma come siamo arrivati a questa risposta? Se ancora non sai o hai domande su come risolvere account come questo, sei nel posto giusto! In questo post insegneremo come dividere i numeri decimali

Esempio 1: dividere il numero 235,7 per 10, per 100 e per 1000.

$\dpi{120} \bg_white 235,7 \div 10 23,57$
$\dpi{120} \bg_white 235,7 \div 100 2,357$
$\dpi{120} \bg_bianco 235,7 \div 1000 0,2357$

Esempio 2: dividere il numero 1,96 per 10, per 100 e per 1000.

$\dpi{120} \bg_bianco 1.96 \div 10 0.196$
$\dpi{120} \bg_bianco 1.96 \div 100 0.0196$
$\dpi{120} \bg_bianco 1.96 \div 1000 0.00196$

Questa regola può essere generalizzata a valori diversi da 10, 100 e 1000. Se, ad esempio, vuoi dividere un numero decimale per 1.000.000, che è un numero di 6 cifre uguale a 0, basta spostare la virgola di sei posizioni verso sinistra.

Divisione da un numero decimale a un numero naturale

Per prima cosa ricordiamo che ogni numero decimale ha una parte intera, formata da unità (U), decine (D), centinaia (C) ecc., e una parte decimale formata da decimi (d), centesimi (c), millesimi (m) ecc.

Detto questo, vediamo un esempio di come dividere un numero decimale per qualsiasi numero naturale.

Esempio: Calcola $\dpi{120} \bg_white 8.25 \div 5$

8 le unità divise per 5 danno 1 unità, che rimane 3 unità.
3 unità = 30 decimi.
30 decimi + 2 decimi (↓ in discesa) = 32 decimi.
32 decimi diviso 5 fa 6, e questo rimane 2 decimi.
Mettiamo la virgola tra l'1 e il 6.
2 decimi = 20 centesimi.
20 cent + 5 cent (↓ in discesa) = 25 cent.
25 centesimi divisi per 5 fa 5 centesimi e non rimane nulla.

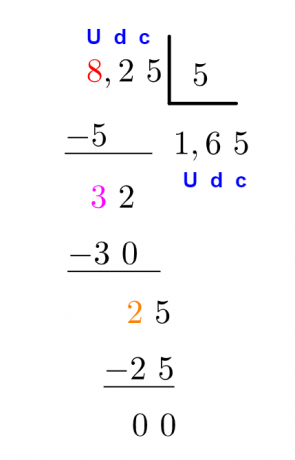
Esiste un metodo alternativo per risolvere questo stesso account. quello che facciamo è cancella la virgola e quindi risolvere il conto di divisione tra numeri naturali.

Per eliminare la virgola:

Moltiplichiamo per 10 se il numero ha un posto dopo la virgola;
Moltiplichiamo per 100 se il numero ha due cifre dopo la virgola;
Moltiplichiamo per 1000 se il numero ha tre cifre dopo la virgola;

E così via.

Poiché 8.25 ha due cifre dopo la virgola, moltiplichiamo per 100:

$\dpi{120} \bg_bianco 8.25 \times 100 825$

Sebbene il numero 5 non abbia una virgola, dobbiamo anche moltiplicarlo per 100. Moltiplichiamo sempre i due numeri di conto, dividendo e divisore, per lo stesso numero.

$\dpi{120} \bg_white 5 \times 100 500$

Quindi risolvi $\dpi{120} \bg_white 8.25 \div 5$ equivale a risolvere $\dpi{120} \bg_white 825 \div 500$ , cioè per risolvere una divisione tra numeri naturali.

Divisione da un numero decimale a un numero decimale

Per dividere un numero decimale per un altro numero decimale, adotteremo la procedura di trasformazione del conto in divisione in numero naturale, eliminando le virgole.

Per eliminare la virgola:

Moltiplichiamo per 10 se il numero ha un posto dopo la virgola;
Moltiplichiamo per 100 se il numero ha due cifre dopo la virgola;
Moltiplichiamo per 1000 se il numero ha tre cifre dopo la virgola;

E così via.

Esempio 1: Calcola $\dpi{120} \bg_white 2.7 \div 0.9$ .

$\dpi{120} \bg_white 2.7 \times 10 27$
$\dpi{120} \bg_white 0.9 \times 10 9$

Poi, $\dpi{120} \bg_white 2.7 \div 0.9 27 \div 9 3$ .

Esempio 2: Calcola $\dpi{120} \bg_white 0.8 \div 0.02$ .

$\dpi{120} \bg_white 0.8 \times 100 80$
$\dpi{120} \bg_white 0.02 \times 100 2$

Nota che anche se il numero 0.8 ha solo un posto dopo la virgola, lo moltiplichiamo per 100. Lo abbiamo fatto perché il numero 0.02 deve essere moltiplicato per 100 ei due numeri di conto devono essere moltiplicati per lo stesso numero.

Così, $\dpi{120} \bg_white 0.8 \div 0.02 80 \div 2 40$ .