
ללמוד לקראת הבחינה מבחן תיכון ארצי (וגם) הוא צעד חשוב למי שרוצה להגיש מועמדות למשרות פנויות בקורסים באוניברסיטה. עם זאת, שלב הלימודים הזה לא תמיד כל כך קל.
בְּ מָתֵימָטִיקָה, קשיים בביצוע חישובים במהירות, שכן הבדיקה מקיפה והזמן קצר, ושינון השונות נוסחאות מתמטיות הן חלק מהתלונות העיקריות של סטודנטים.
ראה עוד
תלמידים מריו דה ז'נרו יתחרו על מדליות באולימפיאדה...
המכון למתמטיקה פתוח להרשמה לאולימפיאדה...
עם זה בחשבון, הכנו את הטקסט הזה עם טיפים וטריקים מתמטיים עבור האויב לכם שרוצים להצליח בבחינה!
בחרנו כמה טיפים חשובים עבורכם שהולכים לקחת את האנם. בדוק את זה למטה!
בְּ הכפל ב-10, 100 ו-1000 או כל חזקה אחרת של 10, יש כמה אסטרטגיות שיזרזו ויפשטו את החישובים במבחן Enem.
ל מספרים שלמים, פשוט הוסף אפסים מימין למספר:
56 × 10 = 560
56 × 100 = 5600
56 × 1000 = 56000
ל מספרים עשרוניים, פשוט העבר את הנקודה העשרונית ימינה לפי מספר האפסים:
9,853 × 10 = 98,53
9,853 × 100 = 985,3
9,853 × 1000 = 9853, = 9853
בְּ חלוקה ב-10, 100 ו-1000 או כל כוח אחר של 10, יש גם כמה אסטרטגיות שיקרבו אותך להצליח ב-Enem.
כאשר שני המספרים מסתיימים באפס, נוכל לבטל את האפסים, מה שמקל על הספירה:
350: 10 = 35: 1 = 35
600: 100 = 6: 1 = 6
29000: 1000 = 29: 1 = 29
ל מספרים עשרוניים, פשוט הזיזו את הנקודה העשרונית שמאלה לפי מספר האפסים:
256,7: 10 = 25,67
256,7: 100 = 2,567
256,7: 1000 = ,2567 = 0,2567
כדי להיות מוכנים יותר עם חשבונות חלוקה, קרא את הטקסט שלנו: טיפים וטריקים לחישובי חלוקה.
א הנוסחה של בהסקרה הוא אחד המפורסמים ביותר במתמטיקה, אך הוא גם נחשב לאחד הקשים ביותר לשינון ולשימוש על ידי תלמידי תיכון רבים.
חלופה לנוסחה של בהסקרה למציאת השורשים של א משוואת מדרגה 2, וה סכום ושיטת המוצר.
סכום (S) והמוצר (P):
S = -b/a ו-P = c/a
חשב את S ו-P מהמקדמים של המשוואה והשורשים הם שני מספרים שהסכום שלהם הוא S והמכפלה היא P.
דוגמא:
x² – 3x – 10
S = -(-3)/1 = 3 ו-P = -10/1 = -10
השורשים הם 5 ו-2, כי 5. -2 = -10 ו-5 + (-2) = 3.
להלן, אנו מציגים כמה טריקים שיעזרו לך לשנן נוסחאות מתמטיות שימושיות מאוד ולזכור אותן במהלך מבחן Enem.
לזכור את העמדה של סינוס, קוסינוס וטנגנס ב מעגל טריגונומטרי, פשוט שנן את החרוז הבא:
"סינוס בעמידה, קוסינוס בשכיבה ומשיק בצד."
אל ה יחסים טריגונומטריים ב משולש ישר זווית לערב את הרגליים הנגדיות והסמוכות ואת תת התחתון. כדי לא להתבלבל עם שלוש הנוסחאות, שנן את המשפט הבא:
"רצתי ונפלתי על קולה."
סינוס = שיתוף/הייp → רץ
קוסינוס = כאן/הייp → נפילה
טנג'נט = שיתוף/כאן ← קולה
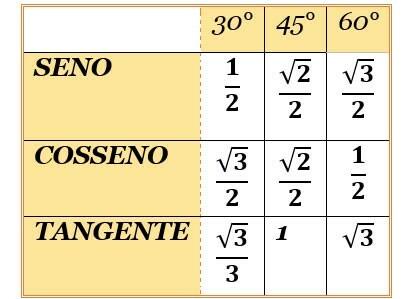
הזוויות הבולטות הן זוויות 30°, 45° ו-60°. הם נקראים כך, בדיוק בגלל שהם כל כך משמשים. אז אתה צריך לשנן את הערכים של פונקציות הסינוס והקוסינוס של זוויות אלה.
כפי ש? יש שיר פשוט:
"אחת שתיים שלוש.
שלוש שתיים אחת.
מתחת כל השניים.
שורש איפה שאין".
זוכרים את השיר הזה, פשוט מרכיבים את השולחן ואין טעות! כדי למצוא את ערכי הטנגנס, פשוט חלקו את הסינוס בקוסינוס.
מתחיל ב נוסחאות חיבור וחיסור קשת, ניתן לפתור בעיות גיאומטריה רבות. עם זאת, בסך הכל, ישנן ארבע נוסחאות והן מאוד דומות.
כדי לא להתבלבל, שנן את המשפט הבא עבור הסינוס:
שב, תגרד! שב, תגרד!
חטא (א+ב) = חטא א. cos b + sin b. כי א
חטא(א – ב) = חטא א. cos b – sin b. כי א
עכשיו לקוסינוס:
גירוד, גירוד! שב, שב!
קוסינוס (a + b) = cos a. cos b + sin a. בלי ב
קוסינוס (א – ב) = cos a. cos b – sin a. בלי ב
ניתוח קומבינטורי בדרך כלל נופל הרבה במבחן Enem. לכן, חיוני להכיר את הנוסחאות של סידור ושילוב, המאפשרים לחשב את מספר האשכולות האפשריים שיכולים להיווצר עם סך של אלמנטים במצבים שונים.
כדי לשנן את הנוסחאות האלה, אתה יכול פשוט לשנן שני משפטים. לסידור, המשפט הוא:
"אאינדה נאל ה פעֶצֶם. לאאל ה! לאאל ה פעֶצֶם!"
ולשילוב:
"Wחבר נאל ה פשיר הלל. לאאל ה! פשיר הלל! לאאל ה פשיר הלל!"
התקדמות אריתמטית (PA) הוא סוג הרצף שנופל הכי הרבה במבחנים. ניתן לזכור את הנוסחה למונח הכללי של AP מהמשפט הבא:
“אאינדה נאל ה המְסוּדָר 1נאָהוּב ראיק!"
“סב נאהוב? אלְאַרגֵן 1נאָהוּב נביצה ו לחלק ל נאתה שתיים!”
אולי יעניין אותך גם: