나머지 부문은 무엇입니까?

영형 나머지 를 구성하는 4가지 요소 중 하나이다. 나누기 알고리즘. 몫이 1이 되기 위해 남은 값입니다. 정수.

나머지가 0이면 나눗셈이 정확하다고 말합니다. 이 경우 배당금은 제수와 몫의 곱과 같습니다.

피제수 = 제수 × 몫

그러나 나머지가 0이 아닌 값인 경우가 있습니다. 예를 참조하십시오.

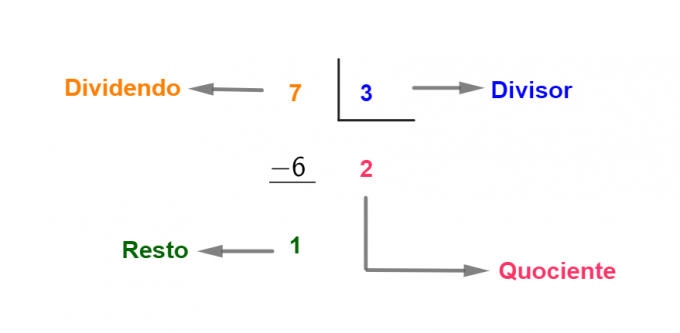
이 경우 피제수는 제수와 몫에 나머지를 더한 값과 같습니다.

피제수 = (제수 × 몫) + 나머지

그러나 결국, 나머지 부문은 무엇입니까? 이 남은 가치는 무엇을 의미합니까? 아래에서 모든 것을 설명하겠습니다!

나머지 부문은 무엇입니까? – 예

두 가지 상황을 포함하는 수학적 문제를 통해 나눗셈의 나머지가 무엇인지 설명합니다.많은 다른.

두 가지 상황의 해결에서 나눗셈 계정은 동일하지만 나머지는 각 상황에서 다른 의미를 가짐을 알 수 있습니다.

문제:

제과업자는 brigadeiros를 생산하고 최대 50개의 사탕을 담을 수 있는 상자에 담아 판매합니다.

어느 날 그녀가 384단위를 생산했다고 가정해 봅시다.

상황 1: 고객은 그날 가지고 있는 미개봉 상자를 모두 구입합니다. 닫힌 상자는 최대 사탕 수를 포함하는 상자입니다.

이 고객은 몇 개의 상자를 받게 됩니까?

해결:

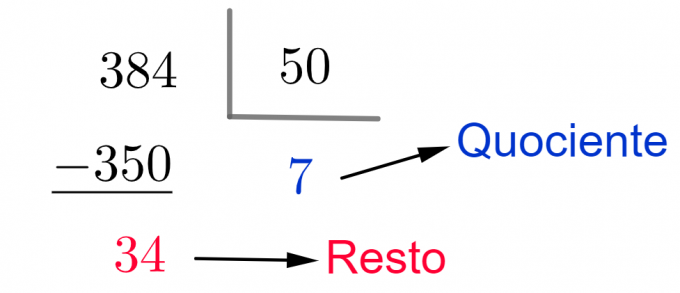
이 계정의 몫은 닫힌 상자의 수를 나타냅니다. 나머지는 새 상자를 완성하기 전에 남은 사탕의 양을 나타냅니다.

고객이 미개봉 상자만 구매하기를 원하므로 7개의 상자를 받게 됩니다.

남은 사탕은 이 고객에게 판매되지 않으므로 나머지는 상자 수에 영향을 미치지 않습니다.

상황 2: 고객은 그날 가지고 있는 과자를 모두 구입합니다.

이 고객은 몇 개의 상자를 받게 됩니까?

해결:

이 상황에서 고객은 과자를 모두 사게 되므로 남은 과자도 상자에 담게 됩니다.

이런 식으로 고객은 8개의 상자를 받게 되며 그 중 7개는 닫혀 있고 다른 상자에는 34개의 사탕이 들어 있습니다.

상황 1과 달리 여기서 나머지는 상자의 수를 방해합니다.

이 문제에서 우리는 어떤 결론을 내릴 수 있습니까?

구분의 나머지는 각 문제 유형에 따라 다른 중요도를 갖습니다. 어떤 경우에는 무시될 수도 있고 그렇지 않은 경우도 있습니다.

당신은 또한 관심이있을 수 있습니다:

• 0으로 나누기
• 분할 연습
• 구분표 - 일상생활에서의 활용과 학습의 이점