Absolute frequentie en relatieve frequentie zijn twee zeer nuttige concepten in data-analyse en Statistiek.
De absolute frequentie komt overeen met het aantal waarnemingen in elke klasse van een variabele. De relatieve frequentie wordt gegeven door het aantal waarnemingen in elke klasse te delen door het totale aantal waarnemingen.
Bekijk meer
Studenten uit Rio de Janeiro strijden om medailles op de Olympische Spelen...
Het Instituut voor Wiskunde staat open voor inschrijving voor de Olympische Spelen...
Bekijk het volgende voorbeeld om echt te begrijpen wat absolute frequentie en relatieve frequentie betekenen en hoe te berekenen:
Om de intentie om te stemmen voor burgemeester in een bepaalde gemeente te peilen, is een enquête gehouden onder 250 kiezers. Er zijn drie burgemeesterskandidaten en elke kiezer antwoordt op welke hij wil stemmen.
Tel na het verkrijgen van de gegevens hoeveel kiezers van plan zijn op elk van de drie kandidaten te stemmen en verkrijg de absolute frequentie voor elke kandidaat:
Als we elke hoeveelheid delen door het totale aantal kiezers, krijgen we relatieve frequentie voor elke kandidaat:
Om de interpretatie te vergemakkelijken, wordt de relatieve frequentie meestal gepresenteerd als a percentage, dus we vermenigvuldigen elk resultaat met 100%.
We kunnen deze gegevens ordenen in een frequentietabel:
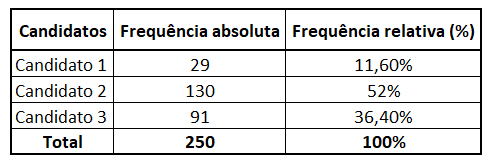
Ook voor een betere visualisatie en begrip van de data kunnen we er wat gebruiken afbeeldingen.
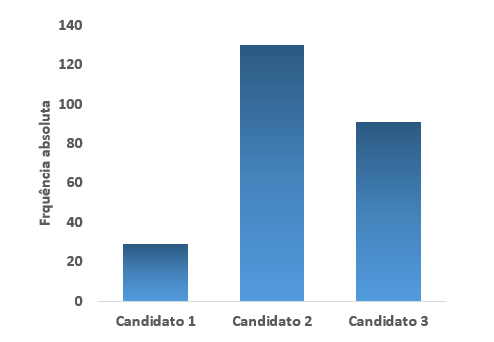
In het staafdiagram vertegenwoordigt elke staaf een klasse en de grootte geeft de absolute frequentie aan die overeenkomt met de klasse.
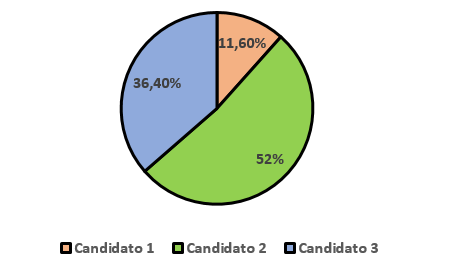
Bij de taartpunten of "pizza", elke sector vertegenwoordigt de klasse in relatie tot het geheel, dat wil zeggen in relatie tot het totale aantal waarnemingen. Over het algemeen wordt hier ook de relatieve frequentie in procenten gebruikt.
Mogelijk bent u ook geïnteresseerd: