Jak uprościć ułamki - Ułamki równoważne i nieredukowalne

Co to znaczy uprościć ułamek? Uproszczenie ułamka oznacza zapisanie równoważnego ułamka, który ma mniejszy licznik i mianownik niż oryginalny ułamek.

Równoważne ułamki to nic innego jak ułamki reprezentujące tę samą ilość lub część całości.

Zobacz więcej

Studenci z Rio de Janeiro powalczą o medale na igrzyskach olimpijskich…

Instytut Matematyki rozpoczyna rejestrację na Igrzyska Olimpijskie…

Aby zrozumieć, jak to działa, rozważ następujący przykład:

W 8-częściowej pizzy ułamek reprezentujący połowę pizzy wynosi $\dpi{120} \frac{4}{8}$ . Jeśli jednak ta sama pizza zostanie podzielona na zaledwie 4 kawałki, połowa będzie reprezentowana przez ułamek $\dpi{120} \frac{2}{4}$ . Zobacz rysunek poniżej: Równoważne ułamki

Pomimo posiadania różnych liczników i mianowników, ułamki zwykłe $\dpi{120} \frac{4}{8}$ To jest $\dpi{120} \frac{2}{4}$ reprezentują taką samą ilość pizzy. Zatem ułamki te są równoważne, co oznacza, że:

$\dpi{120} \frac{4}{8} \frac{2}{4}$

Pytanie 1: Czy istnieje ułamek równoważny ułamkowi $\dpi{120} \frac{2}{4}$ , z jeszcze mniejszymi warunkami?

tak, ułamek $\dpi{120} \frac{1}{2}$ jest równoważny ułamkowi $\dpi{120} \frac{2}{4}$ , ponieważ reprezentuje również połowę pizzy, gdy jest podzielona na tylko dwa kawałki.

Zatem te trzy ułamki są równoważne: $\dpi{120} \frac{4}{8} \frac{2}{4}\frac{1}{2}$ Pytanie 2: Czy istnieje ułamek równoważny ułamkowi $\dpi{120} \frac{1}{2}$ , z jeszcze mniejszymi warunkami?

Nie, to są najmniejsze możliwe wartości, czyli nie możemy już upraszczać tego ułamka.

W tym przypadku mówimy, że ułamek $\dpi{120} \frac{1}{2}$ i nieredukowalna forma ułamka $\dpi{120} \frac{4}{8}$ .

Projekt koła ułatwił znalezienie równoważnych ułamków z mniejszymi wyrazami reprezentującymi połowę ciasta.

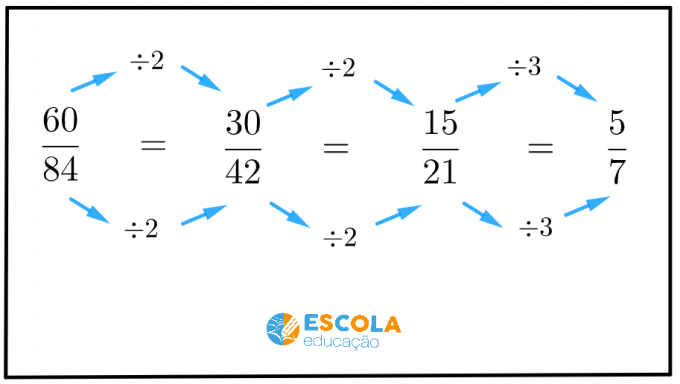
Zobaczmy teraz praktyczny i łatwy sposób na uproszczenie ułamków bez pomocy ilustracji.

Jak uprościć ułamek?

Aby uprościć ułamek, podziel licznik i mianownik ułamka przez a ten sam numer większy niż 1.

Przykład 1: Upraszczamy ułamek $\dpi{120} \frac{3}{12}$ .

Pierwsza liczba większa od 1 to liczba 2. Czy oba wyrazy tego ułamka są podzielne przez 2?

3 nie jest podzielne przez 2, ponieważ reszta z dzielenia nie jest równa zeru;
12 jest podzielne przez 2, ponieważ reszta z dzielenia wynosi zero.

Te dwie liczby muszą być podzielne! Jeśli oba nie są, przejdźmy do następnego numeru.

Następna liczba to 3. Czy oba wyrazy tego ułamka są podzielne przez 3?

3 jest podzielne przez 2, ponieważ reszta z dzielenia wynosi zero;
Liczba 12 jest podzielna przez 3, ponieważ reszta z dzielenia wynosi zero.

Aby uprościć ułamek, podzielmy licznik i mianownik przez 3.

Dlatego musimy $\dpi{120} \frac{3}{12}\frac{1}{4}$ .

Pytanie: Ułamek można uprościć $\dpi{120} \frac{1}{4}$ ? Nie, to są najmniejsze możliwe wyrazy tego ułamka.

Następnie, $\dpi{120} \frac{1}{4}$ jest nieredukowalną postacią ułamka $\dpi{120} \frac{3}{12}$ .

Przykład 2:Upraszczamy ułamek $\dpi{120} \frac{45}{120}$ .

Następnie, $\dpi{120} \frac{45}{120}\frac{3}{8}$ .

Przykład 3:Upraszczamy ułamek $\dpi{120} \frac{60}{84}$ .

Musimy $\dpi{120} \frac{60}{84}\frac{5}{7}$ .

Przeczytaj też:

Działania z ułamkami
Jak dodawać i odejmować ułamki zwykłe

Jak uprościć ułamki - Ułamki równoważne i nieredukowalne

Jak uprościć ułamek?

W Rosji powstają bataliony ochotnicze

Pokarmy bogate w białko

Czy potrafisz znaleźć wszystkie 8 planet w wyszukiwarce słów?