Division of decimal numbers

In many situations we need to solve split accounts with decimal numbers. For example, if four pens cost R$11.20, what is the price of each pen?

To find the answer we have to divide a number in decimal form by a natural number: $\dpi{120} \bg_white 11.20 \div 4 2.8$ . So, each pen costs R$2.80.

But how did we arrive at this answer? If you still don't know or have questions about how to solve accounts like this, you're in the right place! In this post, we will teach how to divide decimal numbers.

Example 1: Divide the number 235.7 by 10, by 100 and by 1000.

$\dpi{120} \bg_white 235.7 \div 10 23.57$
$\dpi{120} \bg_white 235.7 \div 100 2.357$
$\dpi{120} \bg_white 235.7 \div 1000 0.2357$

Example 2: Divide the number 1.96 by 10, by 100 and by 1000.

$\dpi{120} \bg_white 1.96 \div 10 0.196$
$\dpi{120} \bg_white 1.96 \div 100 0.0196$
$\dpi{120} \bg_white 1.96 \div 1000 0.00196$

This rule can be generalized to values other than 10, 100 and 1000. If, for example, you want to divide a decimal number by 1,000,000, which is a number with 6 digits equal to 0, just move the decimal point six places to the left.

Division from a decimal number to a natural number

First, let's remember that every decimal number has an integer part, formed by units (U), tens (D), hundreds (C) etc., and a decimal part formed by tenths (d), hundredths (c), thousandths (m) etc.

That said, let's see an example of how to divide a decimal number by any natural number.

Example: Calculate $\dpi{120} \bg_white 8.25 \div 5$

8 units divided by 5 gives 1 unit, and that's left over 3 units.
3 units = 30 tenths.
30 tenths + 2 tenths (↓ going down) = 32 tenths.
32 tenths divided by 5 is 6, and that's left over 2 tenths.
We put the comma between the 1 and the 6.
2 tenths = 20 hundredths.
20 cents + 5 cents (↓ going down) = 25 cents.
25 cents divided by 5 is 5 cents and nothing is left over.

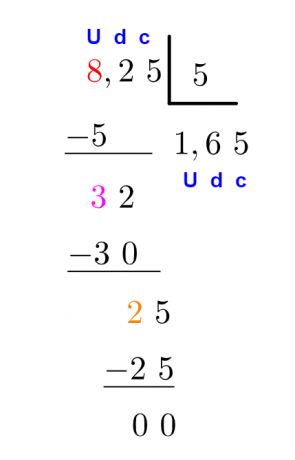
There is an alternative method to resolve this same account. what we do is delete the comma and then solve the division account between natural numbers.

To delete the comma:

We multiply by 10 if the number has a place after the decimal point;
We multiply by 100 if the number has two places after the decimal point;
We multiply by 1000 if the number has three places after the decimal point;

And so on.

Since 8.25 has two places after the decimal point, we multiply by 100:

$\dpi{120} \bg_white 8.25 \times 100 825$

Although the number 5 does not have a comma, we must also multiply it by 100. We will always multiply the two account numbers, dividend and divisor, by the same number.

$\dpi{120} \bg_white 5 \times 100 500$

So solve $\dpi{120} \bg_white 8.25 \div 5$ is the same as solving $\dpi{120} \bg_white 825 \div 500$ , that is, to solve a division between natural numbers.

Division from a decimal number to a decimal number

To divide a decimal number by another decimal number, we will adopt the procedure of transforming the account into natural number division, eliminating the commas.

To delete the comma:

We multiply by 10 if the number has a place after the decimal point;
We multiply by 100 if the number has two places after the decimal point;
We multiply by 1000 if the number has three places after the decimal point;

And so on.

Example 1: Calculate $\dpi{120} \bg_white 2.7 \div 0.9$ .

$\dpi{120} \bg_white 2.7 \times 10 27$
$\dpi{120} \bg_white 0.9 \times 10 9$

Then, $\dpi{120} \bg_white 2.7 \div 0.9 27 \div 9 3$ .

Example 2: Calculate $\dpi{120} \bg_white 0.8 \div 0.02$ .

$\dpi{120} \bg_white 0.8 \times 100 80$
$\dpi{120} \bg_white 0.02 \times 100 2$

Note that even though the number 0.8 only has one place after the decimal point, we multiply it by 100. We did this because the number 0.02 needs to be multiplied by 100 and the two account numbers must be multiplied by the same number.

Thus, $\dpi{120} \bg_white 0.8 \div 0.02 80 \div 2 40$ .

See too:

Division
division algorithm

Portuguese Activity: Verbs in indicative mode

on Jul 22, 2021

Division of decimal numbers

Division from a decimal number to a natural number

Division from a decimal number to a decimal number

Portuguese Activity: Verbs in indicative mode

Portuguese Activity: Linking Verbs

Portuguese Activity: Adverbial tense adjuncts