
A divisionis a basic mathematical operation whose main idea is to divide a quantity into equal parts.
However, there are some situations where the division is not so trivial and presents some “gotchas”, which people tend to miss.
see more
Students from Rio de Janeiro will compete for medals at the Olympics…
The Institute of Mathematics is open for registration for the Olympics…
With that in mind, we have prepared a text on how to make a split.
We'll show you the elements of division, what to do with the remainder, how to do real proof, how to divide by two-digit numbers, how to divide a smaller number by a larger number, and when to add zeros to the quotient.
You division elements are: dividend, divisor, quotient and remainder.
Example: Divide 7 by 3.
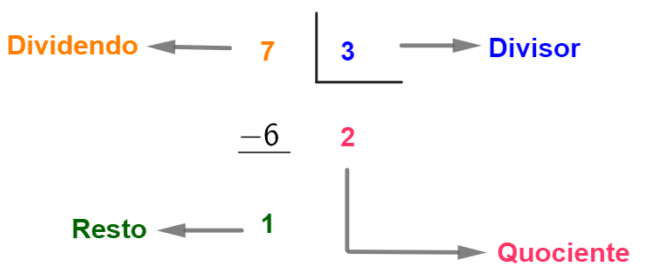
In this account, the dividend is the number 7, the divisor is the number 3, the quotient is 2, and the remainder is 1.
This means that if we divide 7 units into 3 equal parts, each part will be equal to 2 units and there will be 1 unit left over.
To learn more, read our article on division algorithm.
O rest of Division it is a value that can be left over when we carry out a division account. Regarding the rest, we can have two types of divisions.
But what to do with the remainder in non-exact divisions?
If the quotient (division result) has to be a integer, so we stopped the account right there on the rest. The rest may have different meanings depending on the problem.
To understand more about this, read our text What is the rest of the division for?
However, when the result can be a non-integer number, then we can still divide the remainder by the divisor. In the example account, it would be dividing 1 by 3, where the result would be a decimal number.
A real proof in mathematical operations it is a way of checking whether a result obtained is correct or not.
In division with remainder equal to zero, the real proof is to multiply the quotient by the divisor. If the result of this multiplication equals the dividend, then the division account is correct.
dividend = divider× quotient
In division with non-zero remainder, we must still add the remainder to this multiplication, that is:
dividend = divider× quotient + rest
A division with two digits in the divisor is similar to division with a digit in the divisor. What we do is consider the digits of the dividend that form a number greater than the divisor.
See how to do this with an example.
Example: 192 ÷ 16 = ?
19′ 2 | 16
-16 1
03
Note that we didn't divide 192 directly by 16. We consider the first two digits 1 and 9, since 19 is greater than 16.
Then we drop the 2 and continue with the division.
19′ 2 | 16
-16↓ 12
032
-32
00
Actual proof: 16 × 12 = 192.
A division with dividend less than the divisor is a division of a smaller number by a larger number.
To solve this type of math, we add a zero to the dividend and a zero and a comma to the quotient.
If division is still not possible, we add one more zero to the dividend and one more zero to the quotient, and so on, until the dividend is greater than the divisor.
The result of this type of division will always be a decimal number, that is, a number with a comma.
Example: 3 ÷ 60 = ?
3 0 | 60
00000,
Note that 30 is still less than 60. So we add a zero to the dividend and a zero to the quotient. We don't add another comma, the comma is added only once!
3 00 | 60
-3000,05
000
Actual proof: 60 × 0.05 = 3.
In some situations, it is necessary to add zeros to the quotient of a division, such as when going down a number, but it is less than the divisor.
To understand how this works, let's look at some examples.
Example: 1560 ÷ 15 = ?
15′ 60 |15
-15↓↓ 104
00 60
— -60
—-00
Notice that we've brought down the 6, but it's less than 15, so we can't divide. So we add zero to the quotient.
Then we bring down the 0. Now 60 is greater than 15, we can divide.
We arrive at a division with remainder equal to zero, that is, an exact division.
Actual proof: 104 × 15 = 1560.
Example: 302 ÷ 5 = ?
30′ 2 | 5
-30↓ 60
00 2
Notice we've brought down the 2, but it's less than 5, we can't divide. So we add zero to the quotient.
However, see that we don't have any more numbers to go down. So this is a non-exact division with remainder equal to 2.
Actual proof = 60 × 5 + 2 = 300 + 2 = 302.
But if the quotient doesn't need to be a whole number, we can keep dividing and get a decimal number as the quotient.
30′ 2 | 5
-30↓ 60,4
00 20
0-20
0 00
See that we add a zero to the number we want to divide, 2 in this case, and we add a comma in the quotient.
Actual proof: 60.4 × 5 = 302
You may also be interested:


