
Étudier pour l'examen Examen national du lycée (Et soit) est une étape importante pour ceux qui souhaitent postuler à des postes vacants dans des cursus universitaires. Cependant, cette étape des études n'est pas toujours aussi facile.
À mathématiques, des difficultés à effectuer des calculs rapidement, car le test est long et le temps est court, et à mémoriser les différents formules mathématiques sont quelques-unes des principales plaintes des étudiants.
voir plus
Des étudiants de Rio de Janeiro concourront pour des médailles aux Jeux Olympiques…
L'Institut de Mathématiques est ouvert aux inscriptions pour les Jeux Olympiques…
Dans cet esprit, nous avons préparé ce texte avec trucs et astuces mathématiques pour l'enem pour vous qui voulez réussir l'examen !
Nous avons sélectionné quelques précieux conseils pour vous qui allez prendre l'Enem. Découvrez-le ci-dessous!
À Multiplier par 10, 100 et 1000 ou toute autre puissance de 10, il existe des stratégies qui accéléreront et simplifieront les calculs du test Enem.
Pour nombres entiers, ajoutez simplement des zéros à droite du nombre :
56 × 10 = 560
56 × 100 = 5600
56 × 1000 = 56000
Pour Nombres décimaux, il suffit de décaler la virgule vers la droite en fonction du nombre de zéros :
9,853 × 10 = 98,53
9,853 × 100 = 985,3
9,853 × 1000 = 9853, = 9853
À division par 10, 100 et 1000 ou toute autre puissance de 10, il existe également des stratégies qui vous rapprocheront de la réussite dans l'Enem.
Lorsque les deux nombres se terminent par zéro, nous pouvons annuler les zéros, ce qui facilite le comptage :
350: 10 = 35: 1 = 35
600: 100 = 6: 1 = 6
29000: 1000 = 29: 1 = 29
Pour Nombres décimaux, il suffit de déplacer la virgule vers la gauche en fonction du nombre de zéros :
256,7: 10 = 25,67
256,7: 100 = 2,567
256,7: 1000 = ,2567 = 0,2567
Pour être mieux préparé avec les comptes de division, lisez notre texte: Trucs et astuces pour les calculs de division.
UN la formule de bhaskara est l'un des plus célèbres en mathématiques, mais il est également considéré comme l'un des plus difficiles à mémoriser et à utiliser par de nombreux élèves du secondaire.
Une alternative à la formule de Bhaskara pour trouver les racines d'un équation du 2ème degré, et le somme et méthode du produit.
Somme (S) et produit (P) :
S = -b/a et P = c/a
Calculez S et P à partir des coefficients de l'équation et les racines sont deux nombres dont la somme est S et le produit est P.
Exemple:
x² – 3x – 10
S = -(-3)/1 = 3 et P = -10/1 = -10
Les racines sont 5 et -2, car 5. -2 = -10 et 5 + (-2) = 3.
Ci-dessous, nous vous présentons quelques astuces pour vous aider à mémoriser des formules mathématiques très utiles et à vous en souvenir lors du test Enem.
Pour se souvenir de la position de sinus, cosinus et tangente au cercle trigonométrique, mémorisez simplement la rime suivante :
"Sinus debout, cosinus couché et tangente sur le côté."
Au rapports trigonométriques au triangle rectangle impliquer les jambes opposées et adjacentes et l'hypoténuse. Afin de ne pas vous confondre avec les trois formules, mémorisez la phrase suivante :
"J'ai couru et je suis tombé sur la coke."
sinus = co/Salutp → couru
Cosinus = Ici/Salutp → tomber
Tangente = co/Ici → Coca
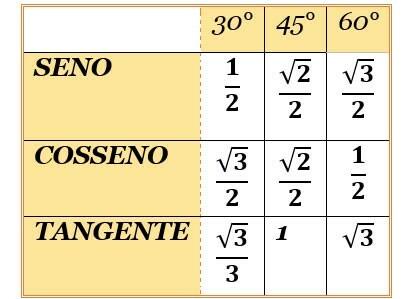
Les angles notables sont les angles de 30°, 45° et 60°. Ils sont appelés ainsi, précisément parce qu'ils sont tellement utilisés. Ainsi, vous devez mémoriser les valeurs des fonctions sinus et cosinus de ces angles.
Comme? Il y a une chanson simple :
"Un, deux, trois.
Trois deux un.
En dessous, c'est tous les deux.
Racine là où il n'y en a pas.
En vous souvenant de cette chanson, il suffit d'assembler la table et il n'y a pas d'erreur! Pour trouver les valeurs de tangente, il suffit de diviser le sinus par le cosinus.
À partir de formules d'addition et de soustraction d'arc, de nombreux problèmes de géométrie peuvent être résolus. Cependant, en tout, il existe quatre formules et elles se ressemblent beaucoup.
Afin de ne pas vous tromper, mémorisez la phrase suivante pour le sinus :
Asseyez-vous, grattez! Asseyez-vous, grattez !
Sin (a + b) = sin a. cos b + sin b. car un
Sin(a – b) = sin a. cos b – péché b. car un
Maintenant pour le cosinus :
Démangeaison, démangeaison! Asseyez-vous, asseyez-vous!
Cosinus (a + b) = cos a. cos b + sin a. sans b
Cosinus (a – b) = cos a. cos b – sin a. sans b
Analyse combinatoire tombe généralement beaucoup dans le test Enem. Il est donc indispensable de connaître les formules de agencement et combinaison, qui permettent de calculer le nombre de clusters possibles pouvant être formés avec un total d'éléments dans différentes situations.
Pour mémoriser ces formules, vous pouvez simplement mémoriser deux phrases. Pour l'arrangement, la phrase est :
"UNtoujours nau Pos. Nonau! Nonau Pos!"
Et pour la combinaison :
"Wami nau Pode. Nonau! Pode! Nonau Pode!"
progression arithmétique (PA) est le type de séquence qui tombe le plus dans les tests. La formule du terme général d'un AP peut être rappelée à partir de la phrase suivante :
“UNtoujours nau Learrangé 1nbien-aimé ric! »
“sdans naimé? UNorganiser 1nbien-aimé nœuf et diviser pour ntoi deux!”
Vous pouvez également être intéressé :


