
Belajar untuk ujian Ujian Nasional SMA (Dan lainnya) merupakan langkah penting bagi mereka yang ingin melamar lowongan di program universitas. Namun, tahap studi ini tidak selalu mudah.
Pada matematika, kesulitan dalam melakukan perhitungan dengan cepat, karena ujiannya luas dan waktunya singkat, serta menghafal yang bermacam-macam rumus matematika adalah beberapa keluhan utama dari siswa.
lihat lebih banyak
Siswa dari Rio de Janeiro akan bersaing memperebutkan medali di Olimpiade…
Institut Matematika membuka pendaftaran untuk Olimpiade…
Dengan mengingat hal itu, kami menyiapkan teks ini dengan tips dan trik matematika untuk enem untuk kamu yang ingin sukses dalam ujian!
Kami telah memilih beberapa tips berharga untuk Anda yang akan mengambil Enem. Lihat di bawah ini!
Pada Kalikan dengan 10, 100 dan 1000 atau kekuatan 10 lainnya, ada beberapa strategi yang akan mempercepat dan menyederhanakan perhitungan dalam tes Enem.
Untuk bilangan bulat, cukup tambahkan nol di sebelah kanan angka:
56 × 10 = 560
56 × 100 = 5600
56 × 1000 = 56000
Untuk angka desimal, tinggal geser koma desimal ke kanan sesuai jumlah nolnya :
9,853 × 10 = 98,53
9,853 × 100 = 985,3
9,853 × 1000 = 9853, = 9853
Pada pembagian dengan 10, 100 dan 1000 atau kekuatan 10 lainnya, ada juga beberapa strategi yang akan membuat Anda lebih dekat untuk melakukannya dengan baik di Enem.
Saat kedua angka berakhir dengan nol, kita dapat menghapus angka nol, sehingga lebih mudah untuk dihitung:
350: 10 = 35: 1 = 35
600: 100 = 6: 1 = 6
29000: 1000 = 29: 1 = 29
Untuk angka desimal, tinggal pindahkan koma desimal ke kiri sesuai jumlah nolnya :
256,7: 10 = 25,67
256,7: 100 = 2,567
256,7: 1000 = ,2567 = 0,2567
Untuk lebih siap dengan akun divisi, baca teks kami: Tip dan trik perhitungan pembagian.
A formula bhaskara adalah salah satu yang paling terkenal dalam matematika, tetapi juga dianggap salah satu yang paling sulit dihafal dan digunakan oleh banyak siswa sekolah menengah.
Alternatif formula Bhaskara untuk mencari akar a persamaan derajat 2, dan jumlah dan metode produk.
Jumlah (S) dan produk (P):
S = -b/a dan P = c/a
Hitung S dan P dari koefisien persamaan dan akarnya adalah dua bilangan yang jumlahnya S dan hasil kali P.
Contoh:
x² – 3x – 10
S = -(-3)/1 = 3 dan P = -10/1 = -10
Akarnya adalah 5 dan -2, karena 5. -2 = -10 dan 5 + (-2) = 3.
Di bawah ini, kami sajikan beberapa trik untuk membantu Anda menghafal rumus matematika yang sangat berguna dan mengingatnya selama ujian Enem.
Untuk mengingat posisi sinus, kosinus, dan tangen pada lingkaran trigonometri, hafalkan sajak berikut ini:
“Sine berdiri, cosinus berbaring, dan bersinggungan di samping.”
Ke rasio trigonometri pada segitiga siku-siku melibatkan kaki yang berlawanan dan berdekatan dan sisi miring. Agar tidak bingung dengan ketiga rumus tersebut, hafalkan kalimat berikut ini:
"Aku berlari dan jatuh karena minuman bersoda."
sinus = bersama/Haip → lari
Cosinus = Di Sini/Haip → jatuh
Tangen = bersama/Di Sini → Kokas
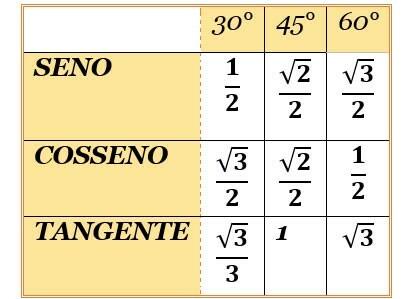
Sudut yang terkenal adalah sudut 30°, 45°, dan 60°. Mereka disebut demikian, justru karena mereka sangat terbiasa. Jadi, Anda perlu menghafal nilai fungsi sinus dan cosinus dari sudut-sudut tersebut.
Sebagai? Ada sebuah lagu sederhana:
"Satu dua tiga.
Tiga dua satu.
Di bawahnya ada dua.
Rooting di mana tidak ada.
Teringat lagu ini, rakit saja mejanya dan tidak ada kesalahan! Untuk mencari nilai tangen, cukup bagi sinus dengan cosinus.
Mulai dari rumus penjumlahan dan pengurangan busur, banyak masalah geometri dapat diselesaikan. Namun, secara keseluruhan, ada empat formula dan sangat mirip.
Agar tidak bingung, hafalkan kalimat berikut untuk sinus:
Duduk, garuk! Duduk, garuk!
Sin (a + b) = sin a. cos b + sin b. karena a
Sin(a – b) = sin a. cos b – sin b. karena a
Sekarang untuk cosinus:
Gatal, gatal! Duduk, duduk!
Cosinus (a + b) = cos a. cos b + sin a. tanpa b
Cosinus (a – b) = cos a. cos b – sin a. tanpa b
Analisis kombinatorial biasanya jatuh banyak di tes Enem. Oleh karena itu, penting untuk mengetahui rumus-rumus dari susunan dan kombinasi, yang memungkinkan menghitung jumlah kemungkinan cluster yang dapat dibentuk dengan total elemen dalam situasi yang berbeda.
Untuk menghafal rumus-rumus tersebut, Anda cukup menghafal dua kalimat. Untuk pengaturan, kalimatnya adalah:
"Abelum Nke Ptulang. TIDAKke! TIDAKke Ptulang!"
Dan untuk kombinasi:
"Wteman Nke Psyair pujian. TIDAKke! Psyair pujian! TIDAKke Psyair pujian!"
perkembangan aritmatika (PA) adalah jenis urutan yang paling banyak jatuh dalam tes. Rumus untuk istilah umum AP dapat diingat dari kalimat berikut:
“Abelum Nke Itudiatur 1Nkesayangan Ric!”
“Sdi dalam Ndicintai? Amengatur 1Nkesayangan Ntelur dan membagi untuk NAnda dua!”
Anda mungkin juga tertarik:


