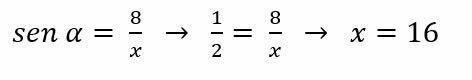Trigonometry is a tool used to calculate distances involving a right triangle. In antiquity, mathematicians used it for calculations performed in astronomy to determine the distance of the Earth from the other Planets.
The similarity of triangles:
see more
Students from Rio de Janeiro will compete for medals at the Olympics…
The Institute of Mathematics is open for registration for the Olympics…
Since the Triangles are polygons, the study carried out to identify the similarity between them is based on the corresponding sides, being proportional and with correspondingly congruent (equal) angles.

The vertices A, B and C correspond, respectively, to the vertices A', B' and C'. Therefore, the ratios of proportionality between the corresponding sides must be set up. Where:
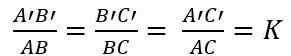
In case all the corresponding sides are proportionally equal, the result of the ratios will be equal to K.
However, the proportionality between the sides and vertices is not enough to determine the similarity between the triangles. It is also necessary that the angles match. Like this:
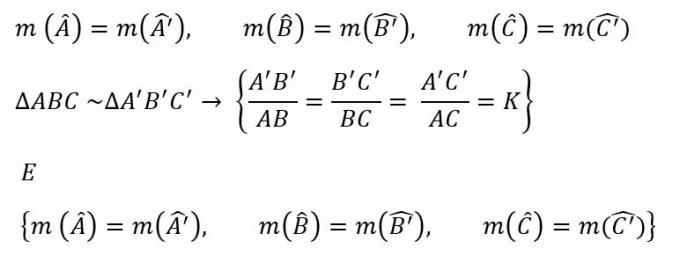
Trigonometric Ratios:
There are three Triangles in Geometry, and they are called; Rectangle, Obtusangle and Acuteangle. Today, we will study the right triangle and for that, there are some properties you should be aware of.
*Before we continue, we must resume that in a Right Triangle the Pythagorean Theorem must be applied, where:
"The square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs"
h² = ca² + co²
h = Hypotenuse
ca = Adjacent leg
co = Opposite leg
To identify the Cathetus and hypotenuse, it is necessary to observe that the hypotenuse is the side opposite the right angle. Watch:
 Angle A:
Angle A:
Hypotenuse – the
Catetes – c and b
Angle B:
Hypotenuse – b
Catetos – c and a
Angle C:
Hypotenuse – c
Catetes – b and a
Sine, Cosine and Tangent:
As we can see in the figure below.

Example:
Since sin α = 1/2, determine the value of x in the right triangle.

The hypotenuse of the triangle is x. Therefore, the side with known measure is the leg opposite the angle α. Then, we have to: